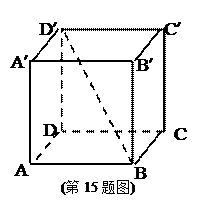(本小题满分14分)
设数列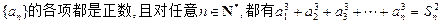 ,
,
其中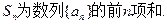
(I)求证: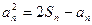 ;
;
(II)求数列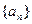 的通项公式;
的通项公式;
(III)设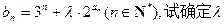 的取值范围,使得对任意
的取值范围,使得对任意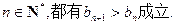
本小题满分13分)
已知函数 =
=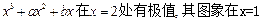 处的
处的 切线平行于直线
切线平行于直线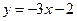 ,试求函数
,试求函数 的极值。
的极值。
已知过A(0,1)和 且与x轴相切的圆只有一个,求
且与x轴相切的圆只有一个,求 的值及圆的方
的值及圆的方 程.
程.
.下图是一几何体的直观图、主视图、俯视图、左视图.
(1)若F为PD的中点,求证:AF⊥面PCD;
(2)证明BD∥面PEC;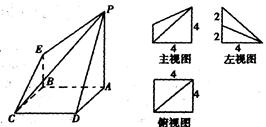
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3)当直线l的倾斜角为45º时,求弦AB的长.
在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为45 0,求:
0,求:
(1)长方体AC¢的高;
(2)长方体AC¢的表面积;
(3)几何体C¢D¢-ABCD的体积.