在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是
A.由加速度的定义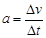 ,当 ,当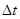 非常小, 非常小,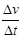 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
B.在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
| D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
如图所示, 和
和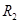 的规格为“4W、100Ω”,
的规格为“4W、100Ω”,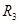 的规格为“1W、100Ω”,当A、B端加电源通电时,这部分电路允许消耗的最大功率为()
的规格为“1W、100Ω”,当A、B端加电源通电时,这部分电路允许消耗的最大功率为()
A.1.25W B.1.5W C.3W D.9W
如图所示,当滑动变阻器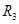 的滑动片向右移动时,两电压表示数变化的绝对值分别是
的滑动片向右移动时,两电压表示数变化的绝对值分别是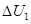 和
和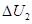 ,则下列结论正确的是 ()
,则下列结论正确的是 ()
A.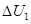 > >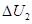 |
B.电阻R1的功率先增大后减小 |
| C.电阻R2的功率一定减小 | D.电源的输出功率先增大后减小 |
有长度相同,质量相同,材料不同的金属导线A、B各一根。已知A的密度比B的大,A的电阻率比B的小。则A、B两根导线的电阻为( )
A.RA>RB B.RA<RB C.RA= RB D.无法判断
如图所示,平行板电容器的两个极板为A、B,B板接地,使其A板带有电荷量+Q,B板带有电荷量﹣Q,板间电场中有一固定点P,以下说法正确的是()
A.若将B板固定,A板下移时,P点的电场强度不变,P点电势降低
B.若将B板固定,A板下移时,P点的电场强度增大,P点电势升高
C.若将A板固定,B板上移时,P点的电场强度不变,P点电势降低
D.如果A板固定,B板上移时,P点的电场强度增大,P点电势升高
图中所示是一个平行板电容器,其板间距为d,电容为C,带电量为Q,上极板带正电。现将一个试探电荷q由两极间的A点移动到B点,如图所示,
A.B两点间的距离为S,连线AB与极板间的夹角为30°,则电场力对试探电荷q所做的功等于() A  |
B. |
C. |
D. |