早在19世纪匈牙利物理学家厄缶就明确指出:“沿水平地面 向东运动的物体,其重量(即: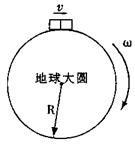 列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称为“厄缶效应” .已知:(1)地球的半径R;(2)地球的自转周期T.如图所示,在地球赤道附近的地平线上,有一列质量是M的列车,如果仅考虑地球自转的影响(列车随地球做线速度为
列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称为“厄缶效应” .已知:(1)地球的半径R;(2)地球的自转周期T.如图所示,在地球赤道附近的地平线上,有一列质量是M的列车,如果仅考虑地球自转的影响(列车随地球做线速度为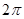 R/T的圆周运动,相对地面静止)时,列车对轨道的压力为N;在此基础上,我们设想,该列车正在以速率v(v为相对地面的速度),沿水平轨道匀速向东行驶.并设此时火车对轨道的压力为N′,那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量(N-N′)为
R/T的圆周运动,相对地面静止)时,列车对轨道的压力为N;在此基础上,我们设想,该列车正在以速率v(v为相对地面的速度),沿水平轨道匀速向东行驶.并设此时火车对轨道的压力为N′,那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量(N-N′)为
A.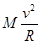 |
B.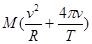 |
C.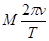 |
D.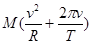 |
起重机吊钩下挂一质量为m的水泥袋,如果水泥袋以加速度n匀减速下降了距离
h,则水泥袋克服钢索拉力做的功为
| A.mgh | B.m(g-a)h |
| C.rn(g+a)h | D.m(a--g)h |
“神舟”六号载人飞船在经过115小时32分钟近八十圈的太空飞行,完成了我国真正意义上有人参与的空间科学实验后,返回舱顺利着陆.“神舟”六号飞船和地球同
A.“神舟”六号的周期长B.“神舟”六号的轨道半径小
C.“神舟”六号的线速度小 D.“神舟”六号的加速度大
一质量为m的物体,从倾角为0的光滑斜面的顶端由静止下滑,下滑时离地面的高度为h,如图所示,当物体滑到斜面底端时,重力的瞬时功率为
A.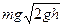 |
B.mg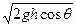 |
C.mg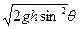 |
D.mg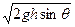 |
如图所示的皮带传动装置中,甲、乙、丙三轮的轴均为水平轴,其中甲、丙两轮半径
相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若
传动中皮带不打滑,则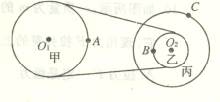
A.A、B两点的线速度大小之比为2:1
B.B、C两点的角速度大小之比为1:2
C.A、B两点的向心加速度大小之比为2:I
D.A、C两点的向心加速度大小之比为I:4
如图所示的装置中,木块B与水平面问的接触是光滑的,子弹A沿水平方向射入
木块后留在木块内,将弹簧压缩到最短.现将子弹、木块和弹簧合在一起作为研究
对象(系统),则此系统在子弹开始射入木块到弹簧压缩至最短的整个过程中
| A.机械能守恒 |
| B.机械能不守恒 |
| C.动能全部转化为弹性势能 |
| D.动能的减少大于弹性势能的增加 |