如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L。一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行。 时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为
时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为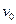 经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置II),导线框的速度刚好为零。此后,导线框下落,经过一段时间回到初始位置I。则
经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置II),导线框的速度刚好为零。此后,导线框下落,经过一段时间回到初始位置I。则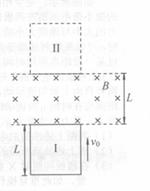
| A.上升过程中,导线框的加速度逐渐增大 |
| B.下降过程中,导线框的加速度逐渐增大 |
| C.上升过程中合力做的功与下降过程中的相等 |
| D.上升过程中克服安培力做的功比下降过程中的多 |
某屋顶为半球形,一人在半球形屋顶上向上缓慢爬行(如图所示),他在向上爬的过程中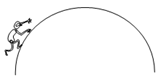
| A.屋顶对他的支持力不变 | B.屋顶对他的支持力变大 |
| C.屋顶对他的摩擦力不变 | D.屋顶对他的摩擦力变大 |
如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d。根据图中的信息,下列判断错误的是
| A.位置“1”是小球释放的初始位置 | B.小球做匀加速直线运动 |
| C.小球下落的加速度为 | D.小球在位置“3”的速度为 |
现在的物理学中加速度的定义式为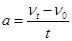 ,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为
,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为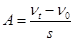 ,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。则下列说法正确的是
,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。则下列说法正确的是
| A.若A不变,则a也不变 |
B.若A不变,则物体在位移中点处的速度比 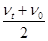 大 大 |
C.若a 不变,则物体在中间时刻的速度为 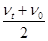 |
| D.若a>0且保持不变,则A逐渐变小 |
图6所示, 小球沿足够长的斜面向上做匀变速运动, 依次经a、b、c、d到达最高点e. 已知ab="bd=6m," bc="1m," 小球从a到c和从c到d 所用的时间都是2s, 设小球经b 、c时的速度分别为vb、vc, 则
、c时的速度分别为vb、vc, 则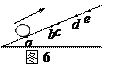
A.vb 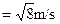 |
B.vc=3m /s /s |
| C.de="3m" | D.从d到e所用时间为4s |
在如图所示的位移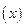 一时间
一时间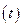 图象和速度
图象和速度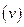 一时间
一时间 图象中,给出的四条图线甲、乙、丙
图象中,给出的四条图线甲、乙、丙 、丁分别代表四辆车由同一地点向同一方向运
、丁分别代表四辆车由同一地点向同一方向运 动的情况,则下列说法正确的是
动的情况,则下列说法正确的是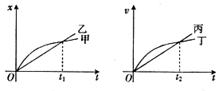
| A.甲车做曲线运动,乙车做直线运动 |
B.0~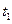 时间内,甲车通过的路程大于乙车 时间内,甲车通过的路程大于乙车 通过的路程 通过的路程 |
C.丙、丁两车在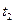 时刻相距最远 时刻相距最远 |
D.0~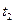 时间内.丙、丁两车的平均速度相等 时间内.丙、丁两车的平均速度相等 |