已知某一区域的地下埋有一根与地表面平行的直线电缆，电缆中通有变化的电流，在其周围有变化的磁场，因此可以通过在地面上测量闭合试探小线圈中的感应电动势来探测电缆的确切位置、走向和深度。当线圈平面平行地面测量时，在地面上a、c两处测得试探线圈中的电动势为零，b、d两处线圈中的电动势不为零；当线圈平面与地面成30°夹角时，在b、d两处测得试探线圈中的电动势为零。经过测量发现，a、b、c、d恰好位于边长为L=1m的正方形的四个顶角上，如图12-15所示。据此可以判定:地下电缆在哪两点连线的正下方？并求出地下电缆离地表面的深度h。
（选考题）如图，ABCD为一竖直平面的轨道，其中BC水平，A点比BC高出10米，BC长1m，AB和CD轨道光滑。一质量为1kg的物体，从A点以4m/s的速度开始运动，经过BC后滑到高出C点10.3m的D点速度为零。求：（g=10m/s2）
（1）物体与BC轨道的动摩擦因数。
（2）物体第3次经过B点的
速度。
（3）物体最后停止的位置（距B点多远）
（4）物体一共经过C点多少次？
如图所示，内壁粗糙的半圆形碗固定在水平地面上，碗的半径R=1m。质量为2kg的小球自碗口静止释放，滑到碗底时的速度大小为v=4m/s。 (g=10m/s2) 则：
（1）从碗口到碗底小球重力势能的变化是多少？
（2）从碗口到碗底摩擦力对小球做功是多少？
（3）在碗底处，小球对碗底的压力是多少？
在水平路上骑摩托车的人，遇到一个壕沟，宽
5m,高度差为0.8m,如图所示，摩托车的速度至少要有多大，才能越过这个壕沟？（g取10m/s2）
一颗质量为m的人造地球卫星绕地球做匀速圆周运动，卫星到地心的距离为r，已知引力常量G和地球质量M，求：
（1）地球对卫星的万有
引力的大小
；
（2）卫星的速度大小.
如图15所示，倾角为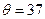
°、电阻不计、间距L=0.3m且足够长的平行金属导轨处在磁感应强度B=1T、方向垂直于导轨平面的匀强磁场中。导轨两端各接一个阻值Ro=2
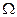的电阻。在平行导轨间跨接一金属棒，金属棒质量m=1kg，电阻r=2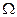,其与导轨间的动摩擦因数
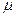=0.5。金属棒以平行于导轨向上的初速度
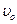=10m/s上滑直至上升到最高点的过程中，通过上端电阻的电荷量
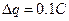(sin37°=0.6，cos37°=0.8,取g=10m/s2)求：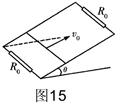
（1）金属棒的最大加速度
（2）上端电阻Ro中产生的热量
（3）金属棒上滑至最高点所用时间