(本小题满分16分)设数列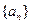 的前n项和为
的前n项和为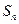 ,数列
,数列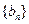 满足:
满足:  ,且数列
,且数列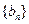 的前
的前
n项和为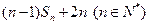 .
.
(1) 求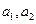 的值;
的值;
(2) 求证:数列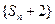 是等比数列;
是等比数列;
(3) 抽去数列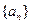 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列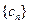 ,若
,若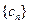 的前n项和为
的前n项和为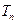 ,求证:
,求证: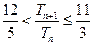 .
.
已知函数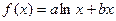
 的图象在点
的图象在点 处的切线的方程为
处的切线的方程为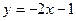 。
。
(I)若对任意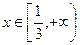 有
有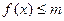 恒成立,求实数
恒成立,求实数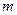 的取值范围;
的取值范围;
(II)若函数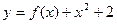 在区间
在区间 内有零点,求实数
内有零点,求实数 的最大值。
的最大值。
已知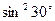 +
+ +
+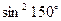 =
=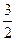 ,
, +
+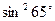 +
+ =
=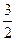 ,
,
通过观察上述两等式,请写出一般性的命题,并给出证明.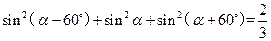
(1 2分)
2分)
已知函数
(1)求函数 在
在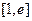 上的最
上的最 大值和最小值.
大值和最小值.
(2)求证:在区间[1,+ ,函数
,函数 的图象,在函数
的图象,在函数 的图象下方。
的图象下方。
一出租车每小时耗油的费用与其车速的立方成正比,当车速为 时,该车耗油的费用为8元/h,其他费用为12元/h.;甲乙两地的公路里程为160km,在不考虑其他因素的前提下,为了使该车开往乙地的总费用最低,该车的车速应当确定为多少公里/小时?
时,该车耗油的费用为8元/h,其他费用为12元/h.;甲乙两地的公路里程为160km,在不考虑其他因素的前提下,为了使该车开往乙地的总费用最低,该车的车速应当确定为多少公里/小时?
已知函数 的图象经过点
的图象经过点 ,曲线在M处的切线恰好与直线
,曲线在M处的切线恰好与直线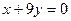 垂直。
垂直。
(I)求实数 的值;
的值;
(II)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。