本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列 中,
中, ,
, .
.
(1)设
 ,证明:数列
,证明:数列 是等差数列;
是等差数列;
(2)设 数列
数列 的前
的前 项和为
项和为 ,求
,求 的值;
的值;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,
, ,是否存在
,是否存在 实数
实数 ,使得对任意的正整数
,使得对任意的正整数 和实数
和实数 ,都有
,都有 成立?请说明理由.
成立?请说明理由.
当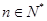 时
时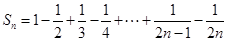 ,
,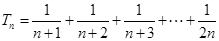
(1)求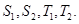
(2)猜想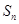 与
与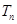 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。
设等差数列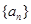 的前n项和为
的前n项和为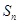 ,已知
,已知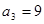 ,
, 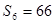 .
.
(1)求数列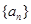 的通项公式
的通项公式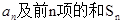 ;
;
(2)设数列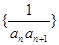 的前n项和为
的前n项和为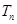 ,证明:
,证明: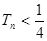 ;
;
如图,已知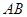 ⊥平面
⊥平面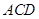 ,
,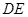 ∥
∥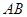 ,
,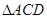 是正三角形,
是正三角形,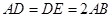 ,且
,且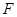 是
是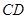 的中点.
的中点.
(Ⅰ)求证: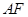 ∥平面
∥平面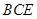 ;
;
(Ⅱ)求证:平面BCE⊥平面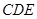 .
.
在 中,已知
中,已知 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 为
为 的中点,求
的中点,求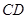 的长.
的长.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计 |
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005] |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)