如图所示,光滑水平地面上方被竖直平面MN分隔成两部分,左边(包括竖直平面MN)有匀强磁场B,右边有匀强电场E0(图中未标)。在O点用长为L=5m的轻质不可伸长的绝缘细绳系一质量mA=0.02kg、带负电且电荷量qA=4×10-4C的小球A,使其在竖直平面内以速度vA=2.5m/s沿顺时针方向做匀速圆周运动,运动到最低点时与地面刚好不接触。处于原长的轻质弹簧左端固定在墙上,右端与质量mB=0.01kg、带负电且电荷量qB=2×10-4C的小球B接触但不连接,此时B球刚好位于M点。现用水平向左的推力将B球缓慢推到P点(弹簧仍在弹性限度内),推力所做的功是W=2.0J,当撤去推力后,B球沿地面向右运动到M点时对地面的压力刚好为零,继续运动恰好能与A球在最低点发生正碰,并瞬间成为一个整体C(A、B、C都可以看着质点),碰撞前后总电荷量保持不变,碰后瞬间匀强电场大小变为E1=1×103 N/C,方向不变。g=10m/s2。求:


(1)匀强磁场的磁感应强度B的大小和方向?
(2)匀强电场的电场强度E0的大小和方向?
(3)整体C运动到最高点时绳对C的拉力F的大小?
如图所示,质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速运动,(g=10N/kg,sin37°=0.6,cos37°=0.8)求:
(1)地面对雪橇的压力大小;
(2)雪橇与水平地面的动摩擦因素的大小。
(10分)一个自由下落的物体,到达地面的速度是39.2m/s,这个物体是从多高落下的?落到地面用了多长时间?(g取9.8m/s2)
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点B点与一条水平轨道相连,轨道是光滑的,轨道所在空间存在水平向右、场强为E的匀强电场,从水平轨道上的A点由静止释放一质量为m带正电的小球,设A、B间的距离为S。已知小球受到的电场力大小等于小球重力的3/4倍,C点为圆形轨道上与圆心O的等高点。(重力加速度为g)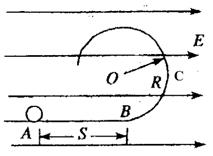
(1)若S=2R,求小球运动到C点时对轨道的压力大小;
(2)为使小球刚好在圆轨道内完成圆周运动,求S的值。
如图所示,四个电阻阻值均为R,电池内阻不计,S闭合时,水平平行的金属板间质量为m,带电荷量为q的微粒,恰好静止在两板的中央d/2处(d为两板间的距离),S断开后,微粒向一极板运动,碰撞后速度大小不变只改变方向,电量由q变为q′,随后向另一极板运动,到达另一极板时速度恰好减为零。
(1)电路中电池电动势多大?
(2)微粒后来的带电荷量q′多大?
如图,电动机M和电灯L并联之后接在直流电源上,电源电动势E=12v,内阻r=1Ω,电动机内阻r’=1Ω,电灯灯丝电阻R=10Ω,理想电压表读数为10v:
(1)流过电源的电流;
(2)电源的输出功率;
(3)电动机对外输出的机械功率。