选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题。如果多做,则按所做的第一题计分。)
22.选修4-1:几何证明选讲
如图,已知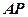 是⊙
是⊙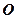 的切线,
的切线, 为切点,
为切点,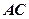 是⊙
是⊙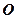 的割线,与⊙
的割线,与⊙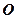 交于
交于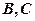 两点,圆心
两点,圆心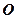 在
在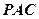 的内部,点
的内部,点
 是
是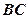 的中点。
的中点。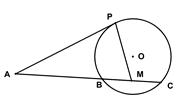
(1)证明 四点共圆;
四点共圆;
(2)求 的大小。
的大小。
23.选修4—4:坐标系与参数方程
已知直线 经过点
经过点 ,倾斜角
,倾斜角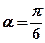 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与曲线
与曲线 相交于两点
相交于两点 ,求点
,求点 到
到 两点的距离之积。
两点的距离之积。
24.选修4—5:不等式证明选讲
若不等式 与不等式
与不等式 同解,而
同解,而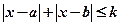 的解集为空集,求实数
的解集为空集,求实数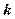 的取值范围。
的取值范围。