已知射线 和点
和点 ,试在
,试在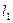 上求一点
上求一点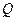 使得
使得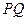 所在直线
所在直线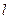 和
和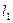 、直线
、直线 在第一象限围成的面积达到最小值,并写出此时直线
在第一象限围成的面积达到最小值,并写出此时直线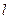 的方程。
的方程。
在直角坐标系xOy中,已知椭圆C: (a >0)与x轴的正半轴交于点P.点Q的坐
(a >0)与x轴的正半轴交于点P.点Q的坐
标为(3,3), =6.
=6.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q且斜率为 的直线交椭圆C于A、B两点,求△AOB的面积
的直线交椭圆C于A、B两点,求△AOB的面积
已知函数f(x)=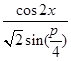 .
.
(Ⅰ)求函数f(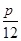 )的值;
)的值;
(Ⅱ)求函数f(x)的单调递减区间.
某教室有4扇编号为a、,b、c、d的窗户和2扇编号为x、y的门,窗户d敞开,其余门和窗户均被关闭.为保持教室空气流通,班长在这些关闭的门和窗户中随机地敞开2扇.
(Ⅰ)记“班长在这些关闭的门和窗户中随机地敞开2扇”为事件A,请列出A包含的基本事件;
(Ⅱ)求至少有1扇门被班长敞开的概率.
在数列{an}中,a1=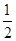 ,点(an,an+1)(n∈N*)在直线y=x+
,点(an,an+1)(n∈N*)在直线y=x+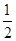 上
上
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=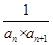 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
已知函数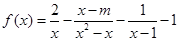
(1)若函数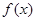 无零点,求实数
无零点,求实数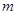 的取值范围;
的取值范围;
(2)若函数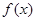 在
在 有且仅有一个零点,求实数
有且仅有一个零点,求实数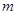 的取值范围
的取值范围