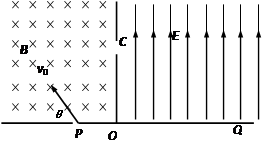如图甲，平行导轨MN、PQ水平放置，电阻不计.两导轨间距d=10cm，导体棒ab、cd放在导轨上，并与导轨垂直.每根棒在导轨间的部分，电阻均为R=1.0Ω.用长为L=20cm的绝缘丝线将两棒系住.整个装置处在匀强磁场中.t=0的时刻，磁场方向竖直向下，丝线刚好处于未被拉伸的自然状态.此后，磁感应强度B随时间t的变化如图乙所示.不计感应电流磁场的影响.整个过程丝线未被拉断.求：
⑴0~2.0s的时间内，电路中感应电流的大小与方向；
⑵t=1.0s的时刻丝线的拉力大小.
如图所示，某货场需将质量m1＝100 kg的货物(可视为质点)从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物由轨道顶端无初速度滑下，轨道半径R＝1.8 m．地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l＝2 m，质量均为m2＝100 kg，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为μ1，木板与地面间的动摩擦因数μ2＝0.2．(最大静摩擦力与滑动摩擦力大小相等，取g＝10 m/s2)
(1)求货物到达圆轨道末端时对轨道的压力大小和方向。
(2)若货物滑上木板A时，木板不动，而滑上木板B时，木板B开始滑动，求μ1应满足的条件．
(3)若μ1＝0.5，求货物滑到木板A末端时的速度和在木板A上运动的时间．
如图所示，在光滑的水平面上停着一辆小车，小车平台的上表面是粗糙的。它靠在光滑的水平桌面旁并与桌面等高。现在有一个质量为m = 2kg的物体C以速度v0 = 10m/s沿水平桌面向右运动，滑过小车平台后从A点离开，恰能落在小车前端的B点。已知小车总质量为M=5kg，O点在A点的正下方，OA=0.8m，OB=1.2m，物体与小车摩擦系数µ = 0.2，g取10m/s2。求：
（1）物体刚离开平台时，小车获得的速度大小。
（2）物体在小车平台上运动的过程中，小车对地发生多大的位移。
如图所示，离地面足够高处有一竖直的空管，质量为2kg，管长为24m，M、N为空管的上、下两端，空管受到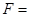
16N竖直向上的拉力作用，由静止开始竖直向下做加速运动，同时在M处一个大小不计的小球沿管的轴线竖直上抛，小球只受重力，取g=10m/s2.求：
（1）若小球上抛的初速度为10m/s，经过多长时间从管的N端穿处?
（2）若此空管的N端距离地面64m高，欲使在空管到达地面时小球必须落到管内，在其他条件不变的前提下，求小球的初速度大小的范围?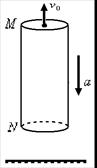
天宫一号于2011年9月29日成功发射，它将和随后发射的神州飞船在空间完成交会对接，实现中国载人航天工程的一个新的跨越。天宫一号进入运行轨道后，其运行周期为T，距地面的高度为h，已知地球半径为R，万有引力常量为G。若将天宫一号的运行轨道看做圆轨道，求：
（1）地球质量M；
（2）地球的平均密度。
(12分)如图所示的区域中，左边为垂直纸面向里的匀强磁场，磁感应强度为 B ，右边是一个电场强度大小未知的匀强电场，其方向平行于OC且垂直于磁场方向．一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中，初速度方向与边界线的夹角θ＝600，粒子恰好从C孔垂直于OC射入匀强电场，最后打在Q点，已知OQ＝ 2 OC ，
不计粒子的重力，求：
( l )粒子从P运动到Q所用的时间 t 。
( 2 )电场强度 E 的大小
( 3 )粒子到达Q点时的动能EkQ