如图所示，平面直角坐标系的y轴竖直向上，x轴上的P点与Q点关于坐标原点O对称，距离为2a。有一簇质量为m、带电量为+q的带电微粒，在
平面内，从P点以相同的速率斜向右上方的各个方向射出（即与x轴正方向的夹角θ，
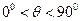），经过某一个垂直于平面向里、磁感应强度大小为
的有界匀强磁场区域后，最终会聚到Q点，这些微粒的运动轨迹关于y轴对称。为保证微粒的速率保持不变，需要在微粒的运动空间再施加一个匀强电场。重力加速度为g。求：
（1）匀强电场场强E的大小和方向；
（2）若微粒在磁场中运动的轨道半径为
，求与
轴正方向成30°角射出的微粒从P点运动到Q点的时间
；
（3）若微粒从P点射出时的速率为v，试推出在
的区域中磁场的边界点坐标与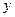
之间满足的关系式。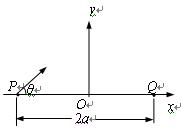
(10分)某型号的舰载飞机在航空母舰的跑道上加速时，发动机产生的最大加速度为5m/s2，所需的起飞速度为50m/s，跑道长100m。通过计算判断，飞机能否靠自身的发动机从舰上起飞？为了使飞机在开始滑行时就有一定的初速度，航空母舰装有弹射装置。对于该型号的舰载飞机，弹射系统必须使它具有多大的初速度？
(8分)一物体做匀变速直线运动，某时刻速率是4m/s，经过1s后的速率是10m/s，那么在这1s内，物体的加速度的大小可能是多少？
(6分)汽车以36km/h的速度行驶，要求在紧急刹车时能在2s内停下来，则刹车时的加速度至少是多少？
(16分)图示为一水平传送装置，由主动轮Q1和从动轮Q2及传送带构成。两轮轴心相距8m，轮与传送带不打滑。现用此装置运送一袋面粉(可视为质点)，已知这袋面粉与传送带之间的动摩擦因数μ＝0.4。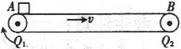
⑴当传送带以4.0rn/s的速度匀速运动时，将这袋面粉由左端Q1正上方A点轻放在传送带上后，这袋面粉由A端运送到Q2正上方的B端所用的时间为多少？
⑵要想尽快将这袋面粉(初速度为零)由A端送到B端，传送带的速度至少为多大？
⑶由于面粉的渗漏，在运送这袋面粉的过程中会在深色传送带上留下白色的面粉痕迹，在满足⑵的情况下，这袋面粉(初速度为零)在传送带上留下的面粉痕迹至少有多长？
(15分)4×100m接力赛是田径比赛中一个激烈的比赛项目，甲、乙两运动员在训练交接棒的过程中发现，甲短距离加速后能保持9m/s的速度跑完全程，为了确定乙起跑的时机，需在接力区前适当的位置设置标记。在某次练习中，甲在接力区前s0处作了标记，当甲跑到此标记时向乙发出起跑口令，乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间)，已知接力区的长度L＝20m，设乙起跑后加速阶段的运动是匀加速运动。
⑴若s0＝13.5m，且乙恰好在速度达到与甲相同时被甲追上，完成交接棒，则在完成交接棒时乙离接力区末端的距离为多大？
⑵若s0＝16m，乙的最大速度为8m/s，并能以最大速度跑完全程，要使甲、乙能在接力区完成交接棒，则乙在听到口令后加速的加速度最大值为多少？