(本小题共14分)
已知椭圆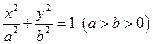 和圆
和圆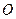 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆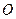 的两条切线,切点分别为
的两条切线,切点分别为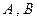 .
.
(Ⅰ)(ⅰ)若圆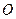 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率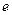
 ;
;
(ⅱ)若椭圆上存在点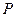 ,使得
,使得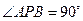 ,求椭圆离心率
,求椭圆离心率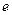 的取值范围;
的取值范围;
(Ⅱ)设直线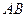 与
与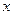 轴、
轴、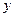 轴分别交于点
轴分别交于点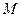 ,
,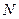 ,求证:
,求证: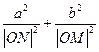 为定值.
为定值.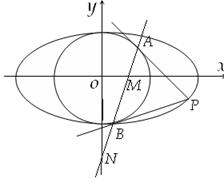
已知x=3是函数f(x)=alnx+x2-10x的一个极值点.
(1)求实数a;
(2)求函数f(x)的单调区间.
已知一个算法如下:
S1输入X;
S2若X<0,执行S3;否则,执行S5;
S3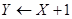 ;
;
S4输出Y,结束;
S5若X=0,执行S6;否则执行S8;
S6 ;
;
S7输出Y,结束;
S8 ;
;
S9输出Y,结束.
(1)指出其功能(用数学表达式表示);
(2)请将该算法用程序框图来描述之.
已知复数 ,
,
(1)如果 是纯虚数,求实数
是纯虚数,求实数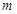 的值;
的值;
(2)设 ,求复数
,求复数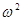 的值.
的值.
设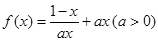 .
.
(1)判断函数 在
在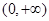 的单调性;
的单调性;
(2)设 为
为 在区间
在区间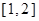 上的最大值,写出
上的最大值,写出 的表达式.
的表达式.
已知函数
 ,函数
,函数
⑴当 时,求函数
时,求函数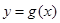 的表达式;
的表达式;
⑵若 ,函数
,函数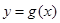 在
在 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值;
⑶在⑵的条件下,求直线 与函数
与函数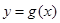 的图象所围成图形的面积.
的图象所围成图形的面积.