(本小题共14分)
已知函数 .
.
(I)判断函数 的单调性;
的单调性;
(Ⅱ)若
 +
+ 的图像总在直线
的图像总在直线 的上方,求实数
的上方,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 与
与 的图像有公共点,且在公共点处的切线相同,求实数
的图像有公共点,且在公共点处的切线相同,求实数 的值.
的值.
设函数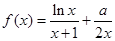 ,
,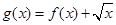 ,若
,若 是函数
是函数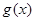 的极值点.
的极值点.
(1)求实数a的值;
(2)若 恒成立,求整数n的最大值.
恒成立,求整数n的最大值.
如图,在四棱锥 中,底面ABCD是菱形,
中,底面ABCD是菱形, ,侧面
,侧面 底面ABCD,并且
底面ABCD,并且 ,F为SD的中点.
,F为SD的中点.
(1)证明: 平面FAC;
平面FAC;
(2)求三棱锥 的体积.
的体积.
某校联合社团有高一学生126人,高二学生105人,高三学生42人,现
用分层抽样的方法从中抽取13人进行关于社团活动的问卷调查.设问题的选择分为“赞同”和“不赞同”两种,且每人都做出了一种选择.下面表格中提供了被调查学生答卷情况的部分信息.
(1)完成下列统计表:
(2)估计联合社团的学生中“赞同”的人数;
(3)从被调查的高二学生中选取2人进行访谈,求选到的两名学生中恰好有一人“赞同”的概率.
已知向量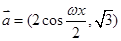 ,
, ,
, ,设函数
,设函数 的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且
的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且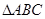 为等边三角形,其高为
为等边三角形,其高为 .
.
(1)求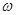 的值及函数
的值及函数 的值域;
的值域;
(2)若 ,且
,且 ,求
,求 的值.
的值.
在直角坐标平面内,直线l过点P(1,1),且倾斜角α= .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A、B两点,求|PA|·|PB|的值.