如图所示,单摆摆球的质量为m,做简谐运动的周期T,摆球从最大位移A处由静止开始释放,摆球运动到最低点B时的速度为v,则 ( )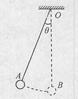
A.摆球从A运动到B的过程中重力的平均功率为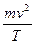 |
B.摆球从A运动到B的过程中重力的冲量为 |
C.摆球运动到B时重力的瞬时功率是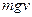 |
D.摆球从A运动到B的过程中合力做的功为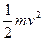 |
 、
、 两个物体从同一地点在同一直线上做匀变速直线运动,它们的速度图象如图所示,则( )
两个物体从同一地点在同一直线上做匀变速直线运动,它们的速度图象如图所示,则( )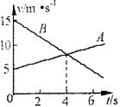
A. 、 、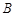 两物体运动方向相反 两物体运动方向相反 |
B.在相遇前,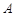 、 、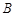 两物体最远距离20m 两物体最远距离20m |
C.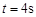 时, 时,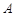 、 、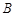 两物体相遇 两物体相遇 |
D.在相遇前,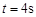 时 时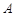 、 、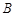 两物体相距最近 两物体相距最近 |
物体沿一直线运动,在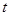 时间内通过的路程为s,它在中间位置
时间内通过的路程为s,它在中间位置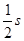 处的速度为
处的速度为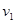 ,在中间时刻
,在中间时刻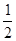 t的速度为
t的速度为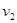 ,则
,则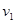 和
和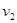 的关系为()
的关系为()
(1)当物体做匀加速直线运动时,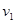 >
>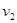 (2)当物体做匀减速直线运动时,
(2)当物体做匀减速直线运动时,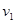 >
>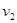
(3)当物体做匀速直线运动时,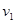 =
=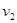 (4)只要物体做匀变速直线运动,
(4)只要物体做匀变速直线运动,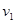 <
<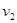
| A.(1)(3) | B.(2)(4) | C.(1)(2)(3) | D.(2)(3)(4) |
一质点做直线运动的位移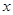 与时间t的关系为
与时间t的关系为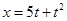 (各物理量均采用国际单位制单位),则该质点()
(各物理量均采用国际单位制单位),则该质点()
A.第1s内的位移是5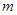 |
B.前2s内的平均速度是6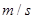 |
C.任意相邻1s内的位移差都是1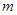 |
D.任意1s内的速度增量都是2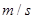 |
伽利略用两个对接的斜面,一个斜面固定,让小球从固定斜面上滚下,又滚上另一个倾角可以改变的斜面,斜面倾角逐渐改变至零,如下图所示.伽利略设计这个实验的目的是为了说明( )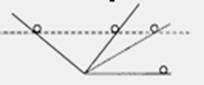
| A.如果没有摩擦,小球将运动到与释放时相同的高度 |
| B.如果没有摩擦,物体运动时机械能守恒 |
| C.维持物体做匀速直线运动并不需要力 |
| D.如果物体不受到力,就不会运动 |
已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动。某时刻在传送带适中的位置冲上一定初速度的物块(如图a),以此时为t=0时刻纪录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2)。已知传送带的速度保持不变,物块与传送带间的μ>tanθ,则

| A.0~t1内,物块对传送带做正功 |
| B.t1~t2内,物块的机械能不断减少 |
C.0~t2内,传送带对物块做功为W= |
| D.系统产生的内能一定大于物块动能的变化量大小 |