为了研究过山车的原理，物理小组提出了下列的设想：取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接，如图所示。一个小物块以初速度
，从某一高处水平抛出，到A点时速度方向恰沿AB方向，并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数
（g取10m/s2，
）
（1）要使小物块不离开轨道，并从水平轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件?
（2）a.为了让小物块不离开轨道，并且能够滑回倾斜轨道AB，则竖直圆轨道的半径应该满足什么条件?
b．按照“a”的要求，小物块进入轨道后可以有多少次通过圆轨道上距水平轨道高为0.01m的某一点。
用电压U和kU通过同距离相同材料的输电线向用户输送同样的总功率。
（1）若要求输电线损失的功率相同，计算前后两种情况输电线的横截面积之比；
（2）若采用同样粗细的导线输电，计算前后两种情况输电线损失的功率之比。
如图所示,在平静的水面下有一点光源S,点光源到水面的距离为H,水对该光源发出的单色光的折射率为n,请解答下列问题:
（1）在水面上方可以看到一圆形的透光面,求该圆的半径.
（2）若该单色光在真空中的波长为λ0,该光在水中的波长为多少?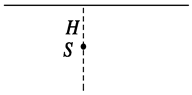
如图，MNP为竖直面内一固定轨道，其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板。M相对于N的高度为h，NP长度为s。一木块自M端从静止开始沿轨道下滑，与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计，物块与NP段轨道间的滑动摩擦因数为
，求物块停止的地方与N点距离的可能值。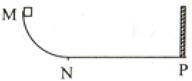
已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，地球自转的周期为24小时，则该行星的自转周期约为多少小时？
如图所示，一高度为h="0.2" m的光滑水平面在A点处与一倾角为θ=30°的光滑斜面连接，一小球以v0=5m/s的速度在平面上向右运动，求小球从A点运动到地面所需的时间，取g=10m/s2。