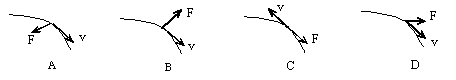图中甲，MN为很大的薄金属板（可理解为无限大），金属板原来不带电。在金属板的右侧，距金属板距离为d的位置上放入一个带正电、电荷量为q的点电荷，由于静电感应产生了如图甲所示的电场分布。P是点电荷右侧，与点电荷之间的距离也为d的一个点，几位同学想求出P点的电场强度大小，但发现问题很难。几位同学经过仔细研究，从图乙所示的电场得到了一些启示，经过查阅资料他们知道：图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的。图乙中两异号点电荷量的大小均为q，它们之间的距离为2d，虚线是两点电荷加线的中垂线。由此他们分别
求出了P点的电场强度大小，一共有以下四个不同的答案（答案中k为静电力常量），其中正确的是 （ ）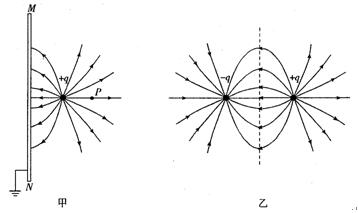
A． |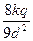
B． |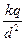
C． |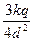
D． |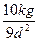
如图所示是甲、乙两球做匀速圆周运动的向心加速度随半径变化的关系图线: （）
| A．甲球运动时线速度大小保持不变 |
| B．乙球运动时线速度大小保持不变 |
| C．甲球运动时角速度大小保持不变 |
| D．乙球运动时角速度大小保持不变 |
同步卫星是指相对于地面不动的人造地球卫星（ ）
| A．它可以是在地面上任一点的正上方，离地心的距离可按需要选择不同值 |
| B．它做圆周运动的周期是24小时。 |
| C．它只能在赤道的正上方，但离地心的距离可按需要选择不同值 |
| D．它只能在赤道的正上方，且离地心的距离是一定的 |
如图所示，在匀速转动的圆筒内壁上，有一物体随圆筒一起转动而未滑动。当圆筒的角速度增大以后，物体仍随圆桶一起匀速转动而不滑动，下列说法正确的是（）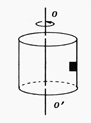
| A．物体所受弹力增大， |
| B．物体所受弹力不变， |
| C．摩擦力减小了 |
| D．摩擦力不变 |
如图所示是一个玩具陀螺，a、b、c是陀螺上的三个点；当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时，下列表述正确的是（）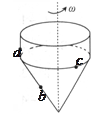
| A．a、b、c三点的线速度大小相等 |
| B．a、b、c三点的角速度相等 |
| C．a、b的角速度比c的大 |
| D．b的线速度比a、c的小 |
一个物体做曲线运动，在某时刻物体的速度v和合外力F的方向可能正确的是（）