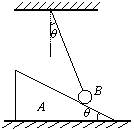
质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,整个系统处于静止状态,已知斜面倾角及轻绳与竖直方向夹角均为θ=30°.不计小球与斜面间的摩擦,则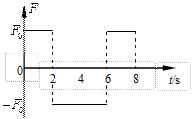
A.轻绳对小球的作用力大小为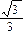 mg mg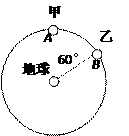 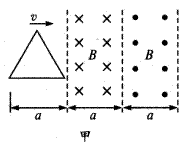   |
B.斜面对小球的作用力大小为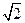 mg mg |
| C.斜面体对水平面的压力大小为(M+m)g | |
D.斜面体与水平面间的摩擦力大小为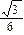 mg mg |
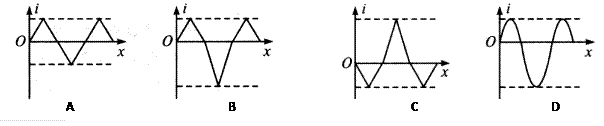
如图一物体沿一直线运动的速度图象,由图象可知 ( ) 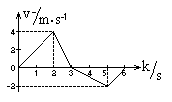
| A.物体运动到t=3s时,离开出发点的距离最远 |
| B.在t=3s时物体改变运动方向 |
| C.0到2s和5到6s两段时间内物体加速度相同 |
| D.运动到t=6s时,物体位移为3m,通过的路程为9m |
下列说法中正确的是()
| A.加速度增大,物体的速度必定增大 |
| B.速度的大小不变,则加速度必定为零 |
| C.物体沿直线向右运动,速度随时间变化,则物体的加速度一定向右 |
| D.加速度的方向不能由速度的方向确定,只能由速度变化的方向来定 |
下列关于位移和路程的说法,正确的是()
| A.位移是矢量,路程是标量,但位移的大小和路程总是相等 |
| B.位移描述直线运动,路程描述曲线运动 |
| C.位移仅取决于始末位置,而路程取决于实际运动路线 |
| D.在某一运动过程中,物体经过的路程总大于或等于物体位移的大小 |
某人坐在甲船中,他看到乙船在运动,那么相对河岸两船的运动情况不可能是()
| A.甲船不动,乙船在运动 | B.甲船运动,乙船不动 |
| C.甲、乙两船都在运动 | D.甲、乙两船运动方向一样,且运动快慢相同 |
他是科学的巨擘、民族的英雄。他是世界著名火箭专家和物理学家,是我国科学技术多个门类的领军人物,取得的成就涵盖工程控制论、卫星、核导弹、系统科学与工程等多方面。所有的荣誉和称号与他取得的伟大成就和对祖国的贡献相比都显得那么的微不足道。不幸的是,巨人在09年10月31日驾鹤仙去。大师虽去,精魂长存!让我们以无比哀痛和崇敬的心情永远记住这位巨人的名字( )
| A.钱学森 | B.高锟 | C.钱永建 | D.吴健雄 |