在2010年青海玉树抗震救灾中，我国自主研制的“北斗一号”卫星导航系统，在抗震救灾中发挥了巨大作用．北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能．“北斗”系统中两颗工作卫星均绕地球做匀速圆周运动，轨道半径为r．某时刻两颗工作卫星分别位于同一轨道上的A、B两位置（如图所示）．若卫星均顺时针运行
，地球表面处的重力加速度为 g，地球半径为 R，则下列说法正确的是
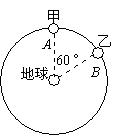
| A．这两颗卫星的加速度大小均为 |
| B．卫星甲向后喷气就一定能追上卫星乙 |
| C．卫星甲由位置 A 运动到位置 B 所需的时间为 |
| D．卫星甲由位置 A 运动到位置B 的过程中万有引力做功为零 |
我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时)；然后，经过两次变轨依次到达“48小时轨道”和“72小时轨道”；最后奔向月球。如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨完成后与变轨前相比，（）
| A．卫星动能增大，引力势能减小 | B．卫星动能增大，引力势能增大 |
| C．卫星动能减小，引力势能减小 | D．卫星动能减小，引力势能增大 |
由于通讯和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的（）
| A．质量可以不同 | B．轨道半径可以不同 |
| C．轨道平面可以不同 | D．速率可以不同 |
据报道，天文学家近日发现了一颗距地球40光年的“超级地球”，名为“55Cancri e”该行星绕母星（中心天体）运行的周期约为地球绕太阳运行周期的
，母星的体积约为太阳的60倍.假设母星与太阳密度相同，“55 Cancri e”与地球均做匀速圆周运动，则“55 Cancri e”与地球的（）
A．轨道半径之比约为 |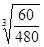
B．轨道半径之比约为 |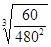
C．向心加速度之比约为 |
D．向心加速度之比约为 |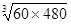
已知地球质量为M，半径为R，自转周期为T，地球同步卫星质量为m，引力常量为G。有关同步卫星，下列表述正确的是（）
A．卫星距离地面的高度为 |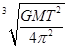
| B．卫星的运行速度小于第一宇宙速度 |
C．卫星运行时受到的向心力大小为 |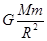
| D．卫星运行的向心加速度小于地球表面的重力加速度 |
为了探测X星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1。随后登陆舱脱离飞船，变轨到离星球更近的半径为r2 的圆轨道上运动，此时登陆舱的质量为m2则（）
A．X星球的质量为 |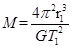
B．X星球表面的重力加速度为 |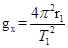
C．登陆舱在r1与r2轨道上运动时的速度大小之比为 |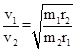
D．登陆舱在半径为r2轨道上做圆周运动的周期为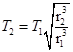 |