原地起跳时,先屈腿下蹲,然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速),加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据:人原地上跳的“加速距离”d1=0.50m,“竖直高度”h1=1.0m;跳蚤原地上跳的“加速距离”d2=0.00080m,“竖直高度”h2=0.10m。假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50m,则人上跳的“竖直高度”是多少?
如左图所示,在真空中足够大的绝缘水平地面上,一个质量为m=0.2kg,带电量为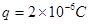 的带正电的小物块处于静止状态,小物块与地面间的动摩擦因数
的带正电的小物块处于静止状态,小物块与地面间的动摩擦因数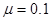 。从t=0时刻开始,空间加上一个如右图所示的场强大小和方向呈周期性变化的电场,(取水平向右的方向为正方向,
。从t=0时刻开始,空间加上一个如右图所示的场强大小和方向呈周期性变化的电场,(取水平向右的方向为正方向,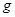 取10m/s2。)求:
取10m/s2。)求:23秒内小物块的位移大小;
3秒内电场力对小物块所做的功
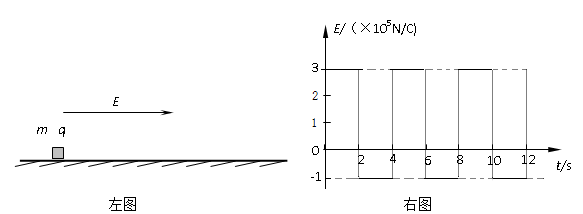
在场强为E =100v/m的竖直向下匀强电场中有一块水平放置的足够大的接地金属板,在金属板的正上方,高为h=0.8m处有一个小的放射源放在一端开口的铅盒内,如图所示。放射物以v0 =200m/s的初速度向水平面以下各个方向均匀地释放质量为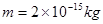 、电量为
、电量为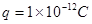 的带正电粒子.粒子最后落在金属板上.不计粒子重力,试求:
的带正电粒子.粒子最后落在金属板上.不计粒子重力,试求: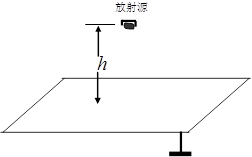
带电粒子下落过程中电场力做的功;
带电粒子打在板上时的动能;
计算落在金属板上的粒子图形的面积大小.(结果保留两位有效数字)
如图所示,电源电动势E=10 V,内阻r=0.5 Ω,“8 V,16 W”的灯泡恰好能正常发光,电动机M绕组的电阻R0=1 Ω,求: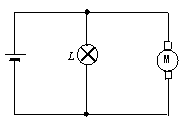
路端电压;
电源的总功率;
电动机的输出功率.
如图所示,将长50cm、质量为10g的均匀金属棒ab的两端用两只相同的弹簧悬挂成水平状态,位于垂直纸面向里的匀强磁场中,当金属棒中通过0.4A电流时,弹簧恰好不伸长,求:匀强磁场中磁感应强度是多大?
当金属棒通过0.2A由a到b的电流时,弹簧伸长1cm,如果电流方向由b到a,而电流大小不变,弹簧伸长又是多少?
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出, yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求: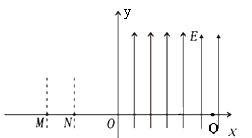
场强E0的大小和方向;
P点的坐标及圆形磁场区的最小半径r;
微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)