一宇宙飞船绕地球做匀速圆周运动,飞船原来的线速度是v1,周期是T1,假设在某时刻它向后喷气做加速运动后,进入新轨道做匀速圆周运动,运动的线速度是v2,周期是T2,则
| A.v1>v2,T1>T2 | B.v1>v2,T1<T2 |
C.v1<v2, T1>T2 T1>T2 |
D.v1<v2,T1<T2 |
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是()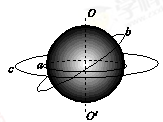
| A.a、b、c的向心加速度大小关系为ab>ac>aa |
| B.a、b、c的向心加速度大小关系为aa>ab>ac |
| C.a、b、c的线速度大小关系为va=vb>vc |
| D.a、b、c的周期关系为Ta=Tc>Tb |
跳台滑雪运动员的动作惊险而优美,其实滑雪运动可抽象为物体在斜坡上的平抛运动。如图所示,设可视为质点的滑雪运动员,从倾角为θ的斜坡顶端P处,以初速度v0水平飞出,运动员最后又落到斜坡上A点处,AP之间距离为L,在空中运动时间为t,改变初速度v0的大小,L和t都随之改变。关于L、t与v0的关系,下列说法中正确的是()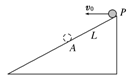
| A.L与v0成正比 | B.L与v02成正比 |
| C.t与v0成正比 | D.t与v02成正比 |
某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tanθ随时间t变化的图像如图所示,则(g取10 m/s2)()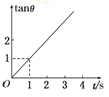
| A.第1 s物体下落的高度为5 m |
| B.第1 s物体下落的高度为10 m |
| C.物体的初速度为5 m/s |
| D.物体的初速度是10 m/s |
一飞船在某行星表面附近沿圆轨道绕该行星飞行。测得周期为T,认为行星是密度均匀的球体,引力常量G已知,据此可推算出()
| A.飞船的轨道半径 | B.飞船的运行速度 |
| C.行星的密度 | D.行星的质量 |
A.B两颗行星,各有一颗卫星,卫星轨道接近各自的行星表面,如果两行星的质量比为MA:MB= q,两行星的半径比为RA:RB= p,则两卫星的周期之比为:()
A. B.q
B.q  C.p
C.p D.q
D.q