如图，四棱锥 S-ABCD的底面是正方形，每条侧棱的长都是地面边长的 
倍，
P为侧棱SD上的点。 
（Ⅰ）求证： AC⊥ SD；
（Ⅱ）若 SD⊥ 平面 PAC，求二面角 P-AC-D的大小
（Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平
面PAC。若存在，求SE：EC的值 
；若不存在，试说明理由。
(
本题满分10分）
已知集合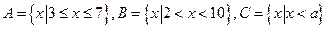
。
（1）求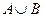
；（2）求
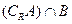；（3）若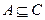
，求a的取值范围.
(本
题满分10分)化简或求值：
（1）
；
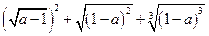（2）
.
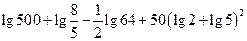（本小题满分10分）选修4－5：不等式选讲
设函数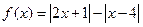
．
（1）解不等式f(x)>0；
（2）若f(x)+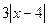
>m对一切实数x均成立，求m的取值范围．
（本小题满分10分）选修4—4：坐标系与参数方程
已知曲线Ｃ１的极坐标方程为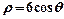
,曲线C2的极坐标方程为
（
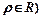，曲线C1，C2相交于点A，B。
（1）将曲线C1，C2的极坐标方程化为直角坐标方程；
（2）求弦AB的长。
（本小题满分10分）选修4—1：几何证明选讲
如图,已知
圆O的直径，C、D是圆O上的两个点，
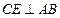于
，
交
于
，交
于
，
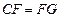
（Ⅰ）求证：C是劣弧BD的中点；
（Ⅱ）求证：
。