设A(a,1)、B(2,b)、C(4,5)为坐标平面上三点,O为坐标原点,若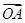 与
与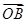 在
在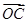 方向上的投影相同,则a与b满足的关系式为( )
方向上的投影相同,则a与b满足的关系式为( )
| A.4a-5b=3 | B.5a-4b=3 |
| C.4a+5b=14 | D.5a+4b=14 |
若非零向量a、b满足|a+b|=|b|,则( )
| A.|2a|>|2a+b| | B.|2a|<|2a+b| |
| C.|2b|>|a+2b| | D.|2b|<|a+2b| |
已知向量a=(2cosθ,2sinθ),b=(0,-2),θ∈ ,则向量a,b的夹角为( )
,则向量a,b的夹角为( )
A. -θ -θ |
B.θ-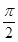 |
C.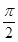 +θ +θ |
D.θ |
设点M是线段BC的中点,点A在直线BC外, 2=16,|
2=16,| +
+ |=|
|=| -
- |,则|
|,则| |=( )
|=( )
| A.8 | B.4 |
| C.2 | D.1 |
已知向量a=( ,1),b是不平行于x轴的单位向量,且a·b=
,1),b是不平行于x轴的单位向量,且a·b= ,则b等于( )
,则b等于( )
A. |
B. |
C. |
D.(1,0) |