如图所示是迈克尔逊用转动八面镜法测光速的实验示意图，图中S为发光点，T是望远镜，平面镜O与凹面镜B构成了反射系统．八面镜距反射系统的距离为AB＝L（L可长达几十千米），且远大于OB以及S和T到八面镜的距离．现使八面镜转动起来，并缓慢增大其转速，当转动频率达到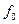
并可认为是匀速转动时，恰能在望远镜中第一次看见发光点S，由此迈克尔逊测出光速c．根据题中所测量的物理量得到光速c的表达式正确的是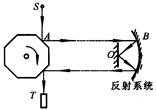
A． |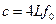
B． |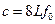
C． |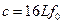
D． |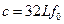
质量为m的钢球自高处落下，以速率v1碰地，竖直向上弹回，碰撞时间极短，离地的速率为v2．在碰撞过程中，钢球受到的冲量的方向和大小为
| A．向下，m（v1－v2） | B．向下，m（v1＋v2） |
| C．向上，m（v1－v2） | D．向上，m（v1＋v2） |
质量为2kg的物体在xoy平面上运动，在x轴方向的速度图像和在y轴方向的位移图像如图所示，下列说法正确的是( )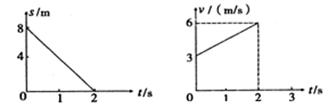
| A．质点的初速度为8m／s |
| B．质点所受的合外力为3N |
| C．t=0时，质点速度方向与合外力方向垂直 |
| D．2s末质点速度大小为6m／s |
开普勒分别于1609年和1619年发表了他发现的行星运动规律，后人称之为开普勒行星运动定律。关于开普勒行星运动定律，下列说法正确的是（）
| A．所有行星绕太阳运动的轨道都是圆，太阳处在圆心上 |
| B．对任何一颗行星来说，离太阳越近，运行速率就越大 |
| C．在牛顿发现万有引力定律后，开普勒才发现了行星的运行规律 |
| D．开普勒独立完成了观测行星的运行数据、整理观测数据、发现行星运动规律等全部工作 |
如图所示，两平行金属板间有一匀强电场，板长为L，板间距离为d，在板右端L处有一竖直放置的光屏M，一带电荷量为q，质量为m的质点从两板中央射入间，最后垂直打在M屏．则下列结论正确的是( )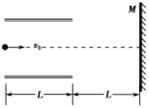
A．板间电场强度大小为 |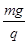
B．板间电场强度大小为 |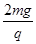
| C．质点在板间的运动时间和它从板的右端运动到光屏的时间相等 |
| D．质点在板间的运动时间大于它从板的右端运动到光屏的时间 |
在地面上空中有方向未知的匀强电场，一带电量为－q的小球以某一速度由M点沿如图所示的轨迹运动到N点．由此可知( )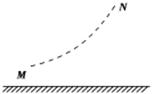
| A．小球所受的电场力一定大于重力 |
| B．小球的动能、电势能和重力势能之和保持不变 |
| C．小球的机械能保持不变 |
| D．小球的动能一定减小 |