(10分)铁路转弯处的弯道半径r是根据地形决定的，弯道处要求外轨比内轨高，其内外轨的高度差h的设计不仅与r有关，还取决于火车在弯道上的行驶速率，表中数据是铁路设计人员技术手册中弯道半径r及与之对应的轨道的高度差h
| 轨道半径r/m |
660 |
330 |
220 |
165 |
132 |
110 |
| 内外轨高度差h/mm |
50 |
100 |
150 |
200 |
250 |
300 |
（1）根据表中数据，试导出h与r关系的表达式，并求出当r=440m时，h的设计值
（2）铁路建成后，火车通过弯道时，要求内外轨均不受车轮施加的侧向压力，又已知我国铁路内外轨间距为L=1435mm，结合表中数据，计算我国火车的转弯速率(取g=10m/s2。结果取整数，路轨倾角很小时，正切值按正弦值计算)
室内装修污染四大有害气体是苯系物、甲醛、氨气和氡。氡存在于建筑水泥、矿渣砖、装饰石材及土壤中。氡看不到，嗅不到，即使在氡浓度很高的环境里，人们对它也毫无感觉。氡进入人的呼吸系统能诱发肺癌，是除吸烟外导致肺癌的第二大因素。静止的氡核
放出一个粒子x后变成钋核
，钋核的动能为Ek1，若衰变放出的能量全部变成钋核和粒子x的动能。试回答以下问题：
①写出上述衰变的核反应方程（请用物理学上规定的符号表示粒子x）；
②求粒子x的动能Ek2。
如图所示，折射率n=
的半圆形玻璃砖置于光屏MN的上方，其平面AB到MN的距离为h=20cm。一束单色光沿图示方向射向圆心O，经玻璃砖后射到光屏上的O′点。现使玻璃砖绕圆心O点顺时针转动，光屏上的光点将向哪个方向移动？光点离O′点最远是多少？
如图，质量为m的小船甲在静止在水面上，一质量为m/3的人站在船尾。另一相同小船乙以速率v0从后方驶来，为避免两船相撞，人从船尾以相对小船甲的速率v水平向后跃到乙船，求速率v至少为多大才能避免两船相撞。
如图所示，一玻璃球体的半径为R，O为球心，AB为直径．来自B点的光线BM在M点射出，出射光线平行于AB，另一光线BN恰好在N点发生全反射．已知∠ABM＝30°，求：
①玻璃的折射率．
②球心O到BN的距离．
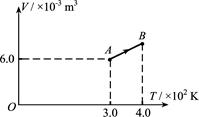
如图所示，一定质量的理想气体从状态A经等压过程到状态B.此过程中，气体压强p＝1.0×105 Pa，吸收的热量Q＝7.0×102 J，求此过程中气体内能的增量．