物块A（可以看成质点）静止在一斜面的底端，斜面倾角a ＝30°，斜面的长为L=1m，物块A与斜面之间的滑动摩擦因数
，斜面固定在水平桌面上。用轻绳跨过斜面顶端的轻滑轮与物块A连接，滑轮与转轴之间的摩擦不计，开始绳刚好绷直，如图所示。若在绳的末端施一竖直向下的恒力F=12N拉绳，物块A由斜面底端到顶端经历的时间为1s。取重力加速度g=10m/s2。
（1）物块A的质量mA是多大？
（2）若物块A静止在斜面底端时，在绳的末端绕过定滑轮挂一质量为1.5kg的物块B由手托住（图中没画出），开始时绳也刚好绷直，则由静止松手后物块A从斜面底端到顶端时B的动能为多少？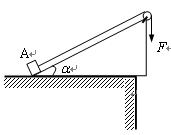
如图所示，质量是20kg的小车，在一个与斜面平行的200N的拉力作用下，由静止开始前进了3m，斜面的倾角为300，小车与斜面间的摩擦力忽略不计．求这一过程物体的重力势能增加了多少?物体的动能增加了多少? 
(19分)某种元素的原子能级图如下图甲所示，当大量处于n = 4能级的原子自发向n = 2的低能级发生能级跃迁时，会发出各种不同频率的光子，试求：
（1）从n = 4能级向n = 2能级跃迁，总共发出多少种光子？
（2）计算(1)问所得到的光子中能量最低的光子的频率．（结果保留一位小数，普朗克常数h = 6.63×10－34J·S）
（3）若用(1)问得到的这些光当中频率较高的两种光（假定命名叫A、B光）来做双缝干涉实验（如下图乙），当用高频率的A光做实验时，在屏幕上的P点出
现二级亮纹（规定中央亮纹为0级亮纹）．不改变实验装置任何部分，换用低频率的B光再做此实验时，P点将出现什么条纹？（要求：先用物理量的字母运算，表达出用B光做实验时应该是亮纹或暗纹的计算式，再代值计算得出数据结果，最后用文字说明是亮纹还是暗纹．即中间过程一律不代值计算）
(17分) 麦克斯韦在1865年发表的（电磁场的动力学理论）一文中揭示了电、磁现象与光的
内在联系及统一性，即光是电磁波．
（1）一单色光波在折射率为1.5的介质中传播，某时刻电场横波图象如图1所示．求该光波的频率．
（2）图2表示一截面为直角三角形的棱镜ABC，∠A = 30o，斜边AB＝a．棱镜材料的折射率为n =
．在此截面所在的平面内，一条光线以45o的入射角从AC边的中点M射入棱镜，求
射出的点的位置（要求作出光路图，不考虑光线沿原路返回的情况）．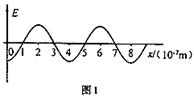
(13分) 如图所示的光电管实验当中，当用波长136.4nm的光照在K上时，调节滑动变阻器，当电压表读数为6.60V时，灵敏电流表读数为零．改用波长65.2nm的光照在K上时，调节滑动变阻器，当电压表读数为16.50V时，灵敏电流表读数为零
．求普朗克常量和K的逸出功．
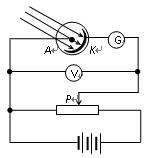
(10分) 一点光源以功率P向外发出波长为λ的单色光，以h表示普朗克恒量，c表示光速．
（1）求光源每秒种发出的光子数目．
（2）若能引起视觉反映的光的最小强度是人的视网膜每秒钟单位面
积上获得n个光子的能量．求当人距离光源多远时将看
不到光源．