(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为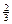 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率
已知函数 . (
. ( 1) 求函数
1) 求函数 的定义域;(2) 求证
的定义域;(2) 求证 在
在 上是减函数;(3) 求函数
上是减函数;(3) 求函数 的值
的值 域.
域.
关于 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围.
的取值范围.
解不等式: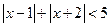
已知函数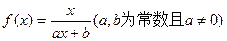 满足
满足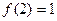 ,且
,且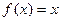 有唯
有唯
一实数解。
(1)求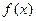 的表达式 ;
的表达式 ;
(2)记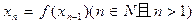 ,且
,且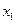 =
=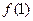 ,求数列
,求数列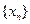 的通项公式。
的通项公式。
(3)记 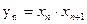 ,数列{
,数列{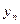 }的前
}的前 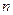 项和为
项和为 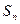 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线 上。
上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn.