x轴上有两点电荷Q1和Q2，Q1和Q2的位置坐标分别为x1、x2。Q1和Q2之间各点对应的电势高低如图中曲线所示，从图中可看出（ ）
| A．Q1的电荷量一定小于Q2的电荷量 |
| B．Q1和Q2一定是同种电荷，但不一定是正电荷 |
| C．电势最低处P点的电场强度为零 |
| D．将一负点电荷由xP点的左侧移至右侧，电场力先做正功后做负功 |
地球同步卫星到地心的距离r可由r3=
求出.已知式中a的单位是m，b的单位是s，c的单位是m/s2，则（）
| A．a是地球半径，b是地球自转的周期，c是地球表面处的重力加速度 |
| B．a是地球半径，b是同步卫星绕地心运动的周期，c是同步卫星的加速度 |
| C．a是赤道周长，b是地球自转的周期，c是同步卫星的加速度 |
| D．a是地球半径，b是同步卫星绕地心运动的周期，c是地球表面处的重力加速度 |
关于开普勒行星运动的公式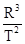
＝k，以下理解正确的是（）
| A．k是一个与行星无关的常量 |
B．若地球绕太阳运转轨道的半长轴为R地，周期为T地；月球绕地球运转轨道的长半轴为R月，周期为T月，则 |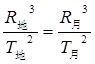
| C．T表示行星运动的自转周期 |
| D．T表示行星运动的公转周期 |
如图所示，a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星，a、b质量相同，且小于c的质量，则（）
| A．b所需向心力最小 |
| B．b、c周期相等，且大于a的周期 |
| C．b、c的向心加速度相等，且大于a的向心加速度 |
| D．b、c的线速度大小相等，且小于a的线速度 |
一宇宙飞船绕地球做匀速圆周运动，飞船原来的线速度是v1，周期是T1，假设在某时刻它向后喷气做加速运动后，进入新轨道做匀速圆周运动，运动的线速度是v2，周期是T2，则（）
| A．v1＞v2，T1＞T2 | B．v1＞v2，T1＜T2 |
| C．v1＜v2，T1＞T2 | D．v1＜v2，T1＜T2 |
两行星A、B各有一颗卫星a和b ，卫星的圆轨道接近各自行星表面，如果两行星质量之比MA：MB=p，两行星半径之比RA：RB＝q则两个卫星周期之比Ta：Tb为 ( )
A． |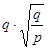
B． |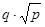
C． |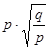
D． |