如图1,是一个空间几何体的三视图,其主(正)视图是一个边长为2的正三角形,俯视图是一个斜边为2的等腰直角三角形,左(侧)视图是一个两直角边分别为
如图1,是一个空间几何体的三视图,其主(正)视图是一个边长为2的正三角形,俯视图是一个斜边为2的等腰直角三角形,左(侧)视图是一个两直角边分别为 和1的直角三角形,则此几何体的体积为
和1的直角三角形,则此几何体的体积为
A. |
B.1 |
C. |
D.2 |
若对任意的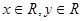 有唯一确定点
有唯一确定点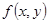 与之对应,则称
与之对应,则称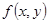 为关于
为关于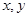 的二元函数,定义:同时满足下列性质的二元函数
的二元函数,定义:同时满足下列性质的二元函数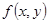 为关于实数
为关于实数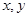 的广义“距离”。
的广义“距离”。
(1)非负性: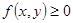 ;
;
(2)对称性: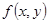 =
=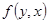 ;
;
(3)三角不等式: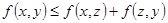 对任意的实数
对任意的实数 均成立。
均成立。
给出下列二元函数:① ; ②
; ②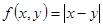 ; ③
; ③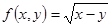 ;
;
④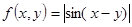 。其中能成为关于实数
。其中能成为关于实数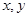 的广义“距离”的函数编号是()
的广义“距离”的函数编号是()
| A.①② | B.① ④ ④ |
C.②③ | D.②④ |
一个几何体的三视图如图,那么该几何体可能是()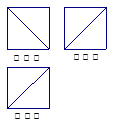
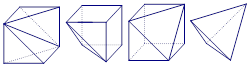
A B C D
设实数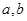 满足
满足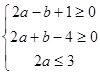 ,则
,则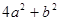 的最大值是()
的最大值是()
| A.25 | B.50 | C.1 | D.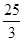 |
若双曲线 的左、右焦点分别为
的左、右焦点分别为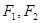 ,线段
,线段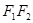 被抛物线
被抛物线 的焦点分成7:5的两段,则此双曲线的离心率为()
的焦点分成7:5的两段,则此双曲线的离心率为()
A.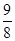 |
B.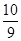 |
C. |
D. |
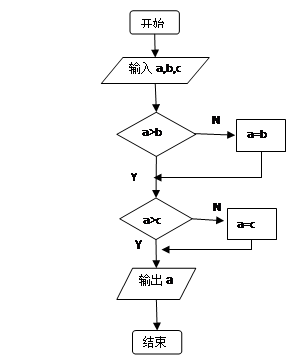
已知 ,则执行右边的程序框图后输出的结果等于( )
,则执行右边的程序框图后输出的结果等于( )
A. |
B. |
C.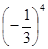 |
D.其它值 |