（原创题）质量为m的卫星在绕地球进行无动力飞行时，它和地球系统的机械能守恒，它们之间势能的表达式是Ep=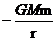
（取无穷远处为势能零点）。现在欲将这颗质量为m的卫星从近地圆轨道发射到近地r1=R，远地r2=3R的椭圆轨道上去，（卫星在这一轨道上的能量和r3=2R的圆周轨道上的能量相同），则需要在近地的A点一次性提供多少能量？（R为地球半径）
如图所示，两平行光滑导轨相距为20cm，与内阻r为0.5Ω的电源相连，导轨平面与水平面成45 o角。整个装置处在方向竖直向下，磁感应强度B为1T的匀强磁场中，当滑动变阻器调至阻值为零时，在导轨上放置一质量为0.2kg的金属棒MN，恰好处于静止状态，经测量，导轨间的金属棒电阻值R为0.5Ω。导轨、导线电阻不计，g取10m/s2
（1）求金属棒所受安培力的大小，并指明金属棒上电流的方向；
（2）计算电源电动势E。
如图所示，半径分别为R和r的甲、乙两个光滑圆形轨道安置在同一竖直平面上，轨道之间有一水平轨道CD相通，一小球以一定的速度先滑上甲轨道，通过动摩擦因数为
的CD段，又滑上乙轨道，最后离开两圆形轨道，若小球在两圆形轨道的最高点的压力都恰好为零，试求CD段的长度？
有一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥。（g取10 m/s2）
（1）汽车到达桥顶时速度为5m/s ，汽车对桥的压力有多大？
（2）汽车以多大速度经过桥顶时便恰好对桥没有压力而腾空？
（3）汽车对地面的压力过小时不安全的，因此从这个角度讲，汽车过桥时的速度不能过大，对于同样的车速，拱桥圆弧的半径大些比较安全，还是小些比较安全？
如图所示，物体在拉力作用下沿水平地面匀速前进．物体的重量用G表示，拉力的大小用F表示，物体与地面间的动摩擦因数用μ表示，拉力与地面间的夹角用θ表示．试回答下列问题:
（1）若上述的F、G、θ为已知量，求物体与地面间的动摩擦因数μ．
（2）若上述的G、μ为已知量，求拉力的最小值．
一辆汽车正在以15m/s的速度行驶，在前方20m处突然亮起红灯，司机立即刹车，刹车过程中汽车的加速度的大小是6m/s2。求：
（1）刹车后3s末汽车的速度
（2）3s末汽车距红绿灯的距离