（本小题满分14分）
如图所示，椭圆C：
的两个焦点为
、
，短轴两个端点为
、
．已知
、
、
成等比数列，
，与
轴不垂直的直线
与C 交于不同的两点
、
，记直线
、
的斜率分别为
、
，且
．
（Ⅰ）求椭圆
的方程；
（Ⅱ）求证直线 与
轴相交于定点，并求出定点坐标；
（Ⅲ）当弦
的中点
落在四边形
内（包括边界）时，求直线 的斜率的取值范围．
已知函数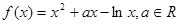
（1）若函数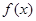
在[1,2]上是减函数,求实数
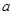的取值范围；
（2）令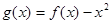
，是否存在实数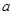，当
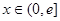时，函数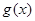
的最小值是3，若存在，求出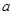的取值；若不存在，说明理由.
已知函数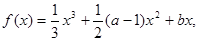
（
为常数）在
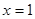和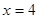
处取得极值，
（1）求函数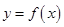
的解析式；
（2）当
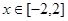时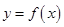，的图像恒在直线
的下方，求实数
的取值范围．
如图，已知椭圆E经过点A（2,3），对称轴为坐标轴，焦点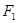
、
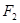在x轴上，离心率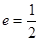
（1）求椭圆E的方程；
（2）求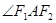
的角平分线所在直线
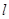的方程.
已知圆C：
和直线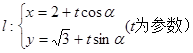
（1）当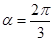
时，求圆上的点到直线
距离的最小值；
（2）当直线与圆C有公共点时，求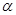
的取值范围.
命题
：对任意实数
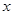都有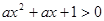
恒成立；命题
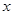：关于的方程
有实数根．若和有且只有一个为真命题，求实数
的取值范围．