如图所示，竖直放置的圆弧轨道和水平轨道两部分相连．水平轨道的右侧有一质量为 2 m的滑块C与轻质弹簧的一端相连，弹簧的另一端固定在竖直的墙M上，弹簧处于原长时，滑块C静止在P点处；在水平轨道上方O处，用长为L的细线悬挂一质量为m的小球B，B球恰好与水平轨道相切，并可绕O点在竖直平面内摆动。质量为m的滑块A由圆弧轨道上静止释放，进入水平轨道与小球B发生弹性碰撞．P点左方的轨道光滑、右方粗糙，滑块A、C与PM段的动摩擦因数均为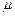
=0.5，A、B、C均可视为质点，重力加速度为g．
（1）求滑块A 从2L高度处由静止开始下滑,与B碰后瞬间B的速度。
（2）若滑块A能以与球B 碰前瞬间相同的速度与滑块C相碰，A至少要从距水平轨道多高的地方开始释放?
（3）在（2）中算出的最小值高度处由静止释放A，经
一段时间A与C相碰，设碰撞时间极短，碰后一起压缩弹簧，弹簧最大压缩量为
L，求弹簧的最大弹性势能。
(8分).如图所示，水平传送带的速度为4.0m/s，它的右端与等高的光滑水平平台相接触.一工件m（可看成质点）轻轻放手传送带的左端，工件与传送带间的动摩擦因数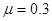
，经过一段时间工件从光滑水平平台上滑出，恰好落在小车左端，已知平台与小车的高度差h=0.8m，小车左端距平台右端的水平距离为s=1.2m，取g=10m/s2，求：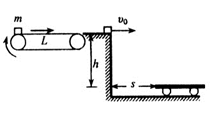
(1)．工件水平抛出的初速度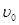
是多少？
(2)．传送带的长度L是多少？
．一辆摩托车能达到的最大速度为30m/s,要想在3min内由静止起沿一条平直公路追上前面1000m处正以20m/s的速度匀速行驶的汽车,则摩托车必须以多大的加速度启动?(保留两位有效数字)
甲同学的解法是:设摩托车恰好在3 min时追上汽车,则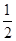
at2=vt+s0,代入数据得a="0.28" m/s2.
乙同学的解法是:设摩托车追上汽车时,摩托车的速度恰好是30m/s,则v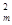
=2as=2a(vt+s0),代入数据得a=0.1m/s2.你认为他们的解法正确吗?若错误,请说明理由,并写出正确的解法.
(8分) 如图：直杆上O1O2两点间距为L,细线O1A长为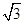
L,O2A长为L,A端小球质量为m，要使两根细线均被拉直，杆应以多大的角速度
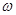转动．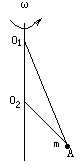 
某市规定,卡车在市区行驶的速度不得超过40km/h。一次一辆飞驰的卡车在危急情况下刹车,经t=1.5s停止,民警量得这一过程中车轮在路面上擦过的痕迹长x=9m,据此能否判断这辆卡车是否超速违章?(设卡车从刹车开始至停下做匀减速直线运动)
一列全长为100米的火车，正在以2m/s2的加速度作匀加速度直线运动，它想要通过正前方一座全长是150米的大桥，当它的车头离桥头还有50米时，它的速度是5m/s，求该火车通过此桥的时间是多少？