地球同步卫星距地面高度为h，地球表面的重力加速度为g，地球半径为R,同步卫星绕地球转动的线速度为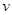
。则地球自转的角速度为ω可表达为（ ）
A． |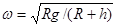
B． |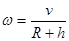
C． |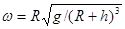
D． |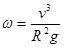
如图所示，细线连接着A球，轻质弹簧两端连接着质量相等的A、B球，在倾角为θ的光 滑斜面体C上静止，弹簧与细线均平行于斜面。C的底面粗糙，在水平地面上能始终保持静止，在细线被烧断后的瞬间，下列说法正确的是( )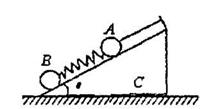
A.两个小球的瞬时加速度均沿斜面向下，大小均为gsinθ
B.A球的瞬时加速度沿斜面向下，大小为2gsinθ
C.C对地面的压力等于A、B和C的重力之和
D.地面对C无摩擦力
长为L的轻绳悬挂一个质量为m的小球，开始时绳竖直，小球与一个倾角θ=45°的静止三角形物块刚好接触，如图所示。现在用水平恒力F向左推动三角形物块，直至轻绳与斜面平行，此时小球的速度速度大小为v，重力加速度为g，不计所有的摩擦。则下列说法中正确的是( )
| A．上述过程中，斜面对小球做的功等于小球增加的动能 |
| B．上述过程中，推力F做的功为FL |
| C．上述过程中，推力F做的功等于小球增加的机械能 |
| D．轻绳与斜面平行时，绳对小球的拉力大小为mgsin45° |
用火箭发射人造卫星，假设火箭由静止竖直升空的过程中，火箭里燃料燃烧喷出气体产生的推力大小不变，空气的阻力也认为不变，则下列图中能反映火箭的速度v或加速度a，随时间t变化的该过程为( )
如图所示，水平地面上固定一个光滑绝缘斜面，斜面与水平面的夹角为θ，一根轻质绝缘细线的一端固定在斜面顶端，另一端系有一个带电小球A，细线与斜面平行。小球A的质量为m、电荷量为q，小球A的右侧固定放置带等量同种电荷的小球B，两球心的高度相同、间距为d，静电力常量为k，重力加速度为g，两带电小球可视为点电荷。小球A静止在斜面上，则（）
A．小球A与B之间库仑力的大小为 |
B．当 时，细线上的拉力为0 |
C．当 时，细线上的拉力为0 |
D．当 时，斜面对小球A的支持力为0 |
如图所示，在正点电荷Q的电场中有M、N、P、F四点，M、N、P为直角三角形的三个顶点，F为MN的中点，∠M＝30°，M、N、P、F四点处的电势分别用φM、φN、φP、φF表示，已知φM＝φN，φF＝φP，点电荷Q在M、N、P三点所在平面内，则（）
| A．点电荷Q一定在MP的连线上 |
| B．连接PF的线段一定在同一等势面上 |
| C．将正试探电荷从P点搬运到N点，电场力做负功 |
| D．φP大于φM |