(本小题满分12分)
已知函数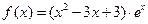 ,其定义域为
,其定义域为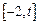 (
(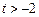 ),设
),设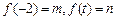 .
.
(Ⅰ)试确定 的取值范围,使得函数
的取值范围,使得函数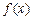 在
在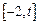 上为单调函数;
上为单调函数;
(Ⅱ)试判断 的大小并说明理由;
的大小并说明理由;
(Ⅲ)求证:对于任意的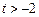 ,总存在
,总存在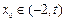 ,满足
,满足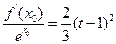 ,并确定这样的
,并确定这样的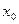 的个数.
的个数.
已知函数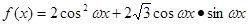 ,(其中
,(其中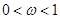 ),若直线
),若直线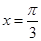 是函数
是函数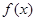 图象的一条对称轴。
图象的一条对称轴。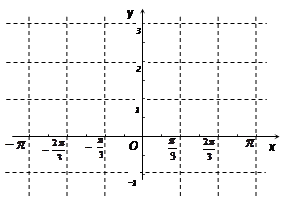
(1)试求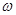 的值;
的值;
(2)先列表再作出函数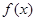 在区间
在区间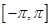 上的图象.
上的图象.
选修4-5:不等式选讲
设不等式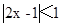 的解集为
的解集为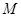 .
.
(1)求集合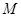 ;
;
(2)若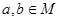 ,试比较
,试比较 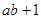 与
与 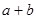 的大小.
的大小.
选修4-4:坐标系与参数方程
在直角坐标系 中,直线L的方程为x-y+4=0,曲线C的参数方程为
中,直线L的方程为x-y+4=0,曲线C的参数方程为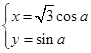
(1)求曲线C的普通方程;
(2)设点Q是曲线C上的一个动点,求它到直线L的距离的最小值.
选修4-1:几何证明选讲
如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O ,E是AB边的中点,EO的延长线交CD于F.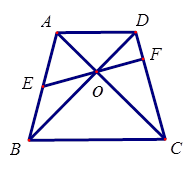
(1)求证:EF⊥CD;
(2)若∠ABD=30°,求证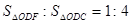
已知函数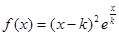 .
.
(1)求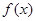 的单调区间;
的单调区间;
(2)若对于任意的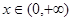 ,有
,有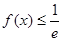 恒成立,求
恒成立,求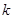 的取值范围.
的取值范围.