下面给出了关于复数的四种类比推理:
① 复数的加减法运算,可以类比多项式的加减法运算法则;
② 由向量 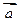 的性质
的性质 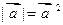 ,可以类比得到复数
,可以类比得到复数 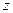 的性质
的性质 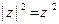 ;
;
③ 方程 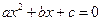 (a 、b 、c ∈ R )有两个不同实根的条件是
(a 、b 、c ∈ R )有两个不同实根的条件是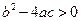 ,类比可以得到 方程
,类比可以得到 方程 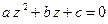 (a 、b 、c ∈ C)有两个不同复数根的条件是
(a 、b 、c ∈ C)有两个不同复数根的条件是 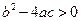 ;
;
④ 由向量加法的几何意义,可以类比得到复数加法的几何意义。
其中类比得到的结论正确的是( *** )
A.① ③ B..② ④ C.② ③ D.① ④
化简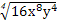 (x<0,y<0)得( )
(x<0,y<0)得( )
| A.2x2y | B.2xy | C.4x2y | D.-2x2y |
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(x)=f( )的所有x之和为( )
)的所有x之和为( )
| A.-3 | B.3 | C.-8 | D.8 |
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo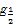 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
| A.是增函数,且f(x)<0 |
| B.是增函数,且f(x)>0 |
| C.是减函数,且f(x)<0 |
| D.是减函数,且f(x)>0 |
已知定义在R上的函数f(x)是偶函数,对x∈R都有f(2+x)=f(2-x),当f(-3)=-2时,f(2007)的值为( )
| A.2 | B.-2 | C.4 | D.-4 |
若偶函数f(x)在(-∞,0)上单调递减,则不等式f(-1)<f(lgx)的解集是( )
| A.(0,10) | B.(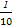 ,10) ,10) |
C.(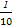 ,+∞) ,+∞) |
D.(0,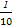 )∪(10,+∞) )∪(10,+∞) |