在上海世界博览会开展期间,计划选派部分高二学生参加宣传活动,报名参加的学生需进行测试,共设4道选择题,规定必须答完所有题,且答对一题得1分,答错一题扣1分,至少得2分才能入选成为宣传员;甲乙丙三名同学报名参加测试,他们答对每个题的概率都为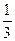 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.
(1)用随机变量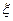 表示能够成为宣传员的人数,求
表示能够成为宣传员的人数,求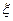 的数学期望与方差;
的数学期望与方差;
(2)若学生甲得分的数值为随机变量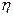 ,求所得分数
,求所得分数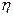 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)
已知 ,函数
,函数 ,
,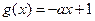 ,
, 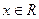 .
.
(I)求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)若在区间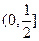 上至少存在一个实数
上至少存在一个实数 ,使
,使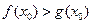 成立,试求正实数
成立,试求正实数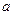 的取值范围.
的取值范围.
(本小题满分12分)
在 中,角
中,角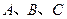 所对的边分别为
所对的边分别为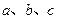 .
.
设向量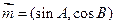 ,
,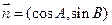
(I)若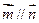 ,求角
,求角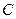 ;
;
(Ⅱ)若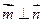 ,
, ,
,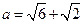 ,求边
,求边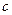 的大小.
的大小.
(本小题满分12分)
已知公差不为零的等差数列 中,
中,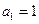 ,且
,且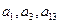 成等比数列.
成等比数列. 
(I)求数列 的通项公式;
的通项公式;
(II)设 ,求数列
,求数列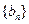 的前
的前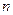 项和
项和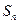 .
.
(本小题满分12分)

已知 ,
, ,
, ,
,
函数 ,且函数
,且函数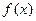 的最小正周期为
的最小正周期为 .
.
(I)求函数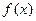 的解析式;
的解析式;
(Ⅱ)求函数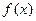 在
在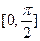 上的单调区间.
上的单调区间.
(本小题满分13分)已知函数 的图象在
的图象在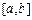 上连续不断,定义:
上连续不断,定义:
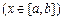 ,
,
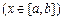 .其中,
.其中,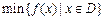 表示函数
表示函数 在
在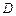 上的最小值,
上的最小值, 表示函数
表示函数 在
在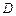 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数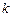 ,使得
,使得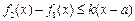 对任意的
对任意的 成立,则称函数
成立,则称函数 为
为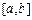 上的“
上的“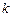 阶
阶 收缩函数”.
收缩函数”.
(1)已知函数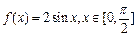 ,试写出
,试写出 ,
, 的表达式,并判断
的表达式,并判断 是否为
是否为 上的“
上的“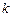 阶收缩函数”,如果是,请求对应的
阶收缩函数”,如果是,请求对应的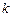 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;
(2)已知 ,函数
,函数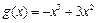 是
是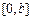 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.