(本小题满分13分)
4位学生与2位教师并坐合影留念,针对下列各种坐法,试问:各有多少种不同的坐法?(用数字做答)
(1)教师必须坐在中间;
(2)教师不能坐在两端,但要坐在一起;
(3)教师不能坐在两端,且不能相邻.
如图,三棱柱 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
(1)求证: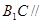 平面
平面 ;
;
(2)求二面角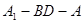 的大小;
的大小;
(3)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 |
乙 |
|
| 9 8 |
8 |
4 8 9 |
| 2 1 0 |
9 |
 6 6 |
(1)求 ;
;
(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
设命题 :函数
:函数 在区间
在区间 上单调递减;命题
上单调递减;命题 :函数
:函数 的最小值不大于0.如果命题
的最小值不大于0.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
设函数
(1)若 时,解不等式
时,解不等式 ;
;
(2)若不等式 的对一切
的对一切 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点 ,求|MA|·|MB|.
,求|MA|·|MB|.