原地起跳时,先屈腿下蹲,然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速)加速过程中重心上升的距离称为"加速距离"。离地后重心继续上升,在此过程中重心上升的最大距离称为"竖直高度"。现有下列数据:人原地上跳的"加速距离"d 1=0.50m,"竖直高度"h 1=1.0m;跳蚤原地上跳的"加速距离"d 2=0.00080m,"竖直高度"h 2=0.10m。假想人具有与跳蚤相等的起跳加速度,而"加速距离"仍为0.50m,则人上跳的"竖直高度"是多少?
如图所示,一束带负电荷e,质量为m的电子流,平行于x轴以速度v0射入第Ⅰ象限区域,为使这束电子能经过x轴上的b点,可在第Ⅰ象限某区域加一个正y方向的匀强电场,场强大小为E,其范围沿y方向无限大,沿x轴方向宽度为s,已知oa=L,ob=2s。求电场边界线跟b点的距离。
如下图所示,BC是半径为R=1m的1/4圆弧形光滑且绝缘的轨道,位于竖直平面内,其下端与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度为E=2.0×10-4N/C,今有一质量为m=1kg、带正电q=1.0×10-4C的小滑块,(体积很小可视为质点),从C点由静止释放,滑到水平轨道上的A点时速度减为零。若已知滑块与水平轨道间的动摩擦因数为μ=0.2,求: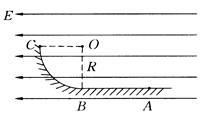
(1)滑块通过B点时的速度大小;
(2)滑块通过B点时圆轨道B点受到的压力大小:
(3)水平轨道上A.B两点之间的距离。
在水平方向的匀强电场中,一不可伸长的不导电细丝一端连着一个质量为m、电荷量为 +q的带电小球,另一端固定在O点,将小球拉起直至细线与场强方向平行,然后无初速度释放,则小球沿圆弧做往复运动.已知小球摆到最低点的另一侧与竖直方向成的最大角度为θ.求: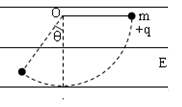
(1)匀强电场的方向和大小;
(2)小球经过最低点时细线对小球的拉力大小.
把一根长为L = 10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中。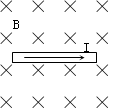
(1)当导线中通以I1 = 2A的电流时,导线受到的安培力大小为 1.0×10-7N,试求该磁场的磁感应强度的大小B。
(2)若该导线中通以I2 = 3A的电流,试求此时导线所受安培力大小F,并判断安培力的方向。
一盏功率为200W的白炽灯泡在300s内有Q=3.0×102C的电荷通过灯丝,求(1)通过灯丝的电流I
(2)灯丝的电阻R;