已知方向向量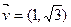 的直线l 过点(
的直线l 过点(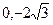 )和椭圆C:
)和椭圆C: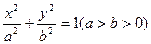 的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。
的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。
(1)求椭圆C的方程;
(2)是否存在过点E(-2,0)的直线m交椭圆C于M、N,满足 (O为原点),若存在求出直线的方程,若不存在,请说明理由。
(O为原点),若存在求出直线的方程,若不存在,请说明理由。
已知y = f (x)是定义在[–1,1]上的奇函数,x∈[0,1]时,f (x) =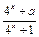 .
.
(1)求x∈[–1,0)时,y = f (x)解析式,并求y = f (x)在[0,1]上的最大值.
(2)解不等式f (x)> .
.
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作l的垂线,垂足为点Q,且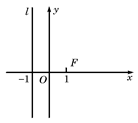
 ·
·
(I)求动点P的轨迹C的方程;
(II)过点F的直线交轨迹C于A、B两点,交直线l于点M.
(1)已知 的值;
的值;
(2)求|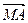 |·|
|·| |的最小值.
|的最小值.
(本小题满分12分)
数列{an}的前N项和为Sn,a1=1,an+1=2Sn (n∈N*).
(I)求数列{an}的通项an;
(II)求数列{nan}的前n项和T.
(本小题满分12分)
设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(I)求f (x)的最小值h(t);
(II)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
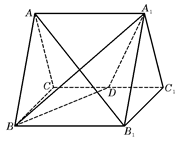 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(I)求证:AB1⊥平面A1BD;
(II)求二面角A-A1D-B的大小.