如图所示,矩形区域I和II内分别存在方向垂直于纸面向外和向里的匀强磁场(AA′、BB′、CC′、DD′为磁场边界,四者相互平行),磁感应强度大小均为B,矩形区域的长度足够长,两磁场宽度及BB′与CC′之间的距离均相同。某种带正电的粒子从AA′上O1处以大小不同的速度沿与O1A成α=30°角进入磁场(如图所示,不计粒子所受重力),当粒子的速度小于某一值时,粒子存区域I内的运动时间均为t0.当速度为v0时,粒子在区域I内的运动时间为t0/5。求: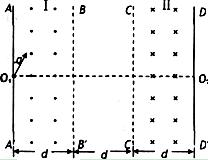
(1)粒子的比荷q/m
(2)磁场区域I和II的宽度d;
(3)速度为v0的粒子从Ol到DD′所用的时间。
如图所示,两平行金属板A、B长l=8cm,两板间距离d=8cm,A板比B板电势高300V,即UAB=300V。一带正电的粒子电量q=10-10C,质量m=10-20kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在中心线上的O点的点电荷Q形成的电场区域(设界面PS右边点电荷的电场分布不受界面的影响)。已知两界面MN、PS相距为L=12cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上。求(静电力常数k=9×109N·m2/C2)
(1)粒子穿过界面PS时偏离中心线RO的距离多远?
(2)点电荷的电量Q。(结果保留三位有效数字)
如图所示,在粗糙水平地面上竖直固定半径为R=6cm的光滑圆轨道。质量为m=4kg的物块静止放在粗糙水平面上A处,物块与水平面的动摩擦因数μ=0.75,A与B的间距L=0.5m。现对物块施加大小恒定的拉力F使其沿粗糙的水平面做直线运动,到达B处将拉力F撤出,物块沿竖直光滑圆轨道运动。若拉力F与水平面夹角为θ时,物块恰好沿竖直光滑圆轨道通过最高点,取重力加速度g=10m/s2,物块可视为质点。求: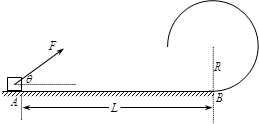
(1)物块到达B处时的动能;
(2)拉力F的最小值及与水平方向的夹角θ。
水平地面上有一质量为m=2kg的木块,放在与墙的距离为x=20m的位置。现用大小为F=20N的水平推力推木块,使木块由静止开始运动,经过t=4s的时间到达墙边。
(1)求木块与水平地面间的动摩擦因数μ;
(2)若仍用大小为20N的水平推力,为使木块能到达墙边,推力作用的最短时间t1为多少?
(3)若仍用大小为20N的力作用于木块,为使木块用最短时间到达墙边,推力作用的最短时间t2为多少?
如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m1 的小球静止在轨道最低点,另一质量为m2 的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1 发生碰撞并粘在一起.求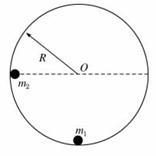
①小球m2 刚要与m1 发生碰撞时的速度大小;
②碰撞后,m1 和m2 能沿内壁运动所能达到的最大高度(相对碰撞点)
一列简谐波沿x轴方向传播,已知x轴上x1=0和x2=1m两处质点的振动图象分别如图(甲)、(乙)所示,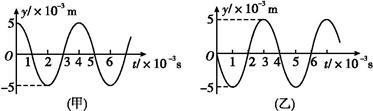
①若此波沿x轴正向传播,则波的传播速度的可能值.
②若此波沿x轴负向传播,则波的传播速度的可能值.