图1所示的装置中,粒子源A产生的初速为零、比荷为 的正离子沿轴线进入一系列共轴且长度依次增加的金属圆筒,奇数和偶数筒分别连接在周期为T、最大值为U0的矩形波电源两端,电源波形如图2所示,离子在每个圆筒内做匀速直线运动的时间等于交变电源的半个周期,在相邻两筒之间受电场力作用被加速(加速时间不计).离子离开最后一个圆筒后垂直于边OE进入磁感应强度为B的匀强磁场,最后从 OF边出射.(不计离子所受重力)
的正离子沿轴线进入一系列共轴且长度依次增加的金属圆筒,奇数和偶数筒分别连接在周期为T、最大值为U0的矩形波电源两端,电源波形如图2所示,离子在每个圆筒内做匀速直线运动的时间等于交变电源的半个周期,在相邻两筒之间受电场力作用被加速(加速时间不计).离子离开最后一个圆筒后垂直于边OE进入磁感应强度为B的匀强磁场,最后从 OF边出射.(不计离子所受重力)
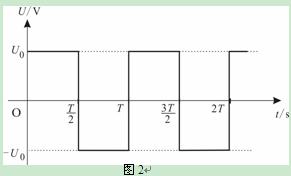
(1)求离子在第一个金属筒内的速率.
(2)求离子在第n个筒内的速率及第n个筒的长度.
(3)若有N个金属筒,求离子在磁场中做圆周运动
的半径.
(4)若比荷为 的离子垂直于OF边出射,要使比
的离子垂直于OF边出射,要使比
荷为 的离子也能垂直于OF边出射,求电源电压最
的离子也能垂直于OF边出射,求电源电压最
大值的改变量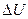 以及磁感应强度的改变量
以及磁感应强度的改变量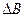 .
.
如图所示的电路中,电源的电动势E=2V,R1=R2=R3=1Ω,当S闭合时,电压表的示数为1V,求:
(1)流过R1和R2的电流;
(2)电源的路端电压和内电阻;
(3)若S断开,电压表的示数变为多少?
如图所示,电源内阻r=1Ω,R1=2Ω,R2=6Ω,灯L上标有“3V、1.5W”的字样,当滑动变阻器R3的滑片P移到最右端时,电流表示数为1A,灯L恰能正常发光。
(1)求电源的电动势;
(2)求当P移到最左端时,电流表的示数;
(3)当滑动阻器的Pb段电阻多大时,变阻器R3上消耗的功率最大?最大值多大?
如图所示,电源的电动势E=10 V,内阻r=1 Ω,电容器的电容C=40 μF,电阻R1=R2=4 Ω,R3=5 Ω.接通开关S,待电路稳定后,求:
(1)理想电压表V的示数;
(2)电容器所带的电荷量.
一个做匀变速直线运动的物体,第一个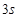 内的位移是
内的位移是 ,第2个
,第2个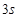 内位移为0,求该物体运动的
内位移为0,求该物体运动的
(1)加速度
(2)初速度
一列长 的列车以
的列车以 的正常速度行驶,当通过
的正常速度行驶,当通过 长的大桥时,必须以
长的大桥时,必须以 的速度行驶。在列车上桥前需提前减速,当列车头刚上桥时速度恰好为
的速度行驶。在列车上桥前需提前减速,当列车头刚上桥时速度恰好为 ,列车全部离开大桥时又需通过加速恢复原来的速度。减速过程中,加速度大小为
,列车全部离开大桥时又需通过加速恢复原来的速度。减速过程中,加速度大小为 ;加速过程中,加速度大小为
;加速过程中,加速度大小为 ,则该列车从减速开始算起,到过桥后速度达到
,则该列车从减速开始算起,到过桥后速度达到 ,共用了多长时间。
,共用了多长时间。