如图所示，足够长的光滑平行金属导轨cd和ef，水平放置且相距L，在其左端各固定一个半径为r的四分之三金属光滑圆环，两圆环面平行且竖直。在水平导轨和圆环上各有一根与导轨垂直的金属杆，两金属杆与水平导轨、金属圆环形成闭合回路，两金属杆质量均为m，电阻均为R，其余电阻不计。整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中。当用水平向右的恒力F=
mg拉细杆
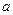，达到匀速运动时，杆b恰好静止在圆环上某处，试求：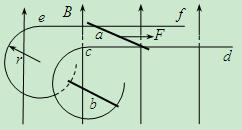
（1）杆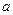做匀速运动时，回路中的感应电流，并在图中杆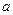上标出感应电流的方向
（2）杆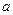做匀速运动时的速度；
（3）杆b静止的位置距圆环最低点
的高度。
有某校一课外活动小组自制一枚火箭，设火箭发射后始终在垂直于地面的方向上运动．火箭点火后可认为做匀加速直线运动，经过4 s到达离地面40 m高处时燃料恰好用完，若不计空气阻力，取g＝10 m/s2，求：燃料恰好用完时火箭的速度
火箭上升离地面的最大高度
飞机着陆后匀减速滑行，它滑行的初速度是60m/s，加速度大小是3m/s2,则：飞机着陆后滑行的时间是多少？
要滑行多远才能停下来？
桌面上放着一个单匝矩形线圈，线圈中心上方一定高度上有一竖直的条形磁铁，此时线圈内的的磁通量为0.04Wb。把条形磁铁竖直放在线圈内的桌面上时，线圈内的磁通量为0.12Wb.分别计算以下两个过程中线圈中的感应电动势. 
把条形磁铁从图中位置在0.4s内放到线圈内的桌面上；
换用100匝的矩形线圈，线圈面积和原单匝线圈相同，把条形
磁铁从图中位置在0.1s内放到线圈内的桌面上。
如图所示，一个质量为m=0.4kg，带电量为q=2.5×10-3C的半径极小的，用绝缘丝线悬挂在某水平匀强电场E中，当小球静止时，测得悬线与竖直方向的夹角为37°，(sin37°=0.6 cos37°=0.8 g="10N/kg)" 试求：
小球受哪几个力而平衡？
匀强电场E的方向；
小球所受电场力的大小及匀强电场E的大小。
如图所示，一小型发电机内有n=100匝矩形线圈，线圈面积S=0.10m2，线圈电阻为1Ω。在外力作用下矩形线圈在B=0.10T匀强磁场中，以恒定的角速度ω=100π rad/s绕垂直于磁场方向的固定轴OO′匀速转动，发电机线圈两端与R =9Ω的电阻构成闭合回路。求
线圈转动时产生感应电动势的最大值
从线圈平面通过中性面时开始，线圈转过90º角的过程中通过电阻R横截面的电荷量
写出电阻R两端电压瞬时值的表示式（当线圈平面与磁场垂直时开始计时）
线圈匀速转动10s，电流通过电阻R产生的焦耳热（π2=10）