如果复数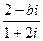 的实部与虚部互为相反数,那么实数
的实部与虚部互为相反数,那么实数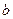 等于
等于
A.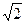 |
B. |
C.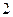 |
D.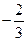 |
某路段检查站监控录像显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如右图的频率分布直方图,则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有 
| A.100辆 | B.200辆 |
| C.300辆 | D.400辆 |
对两个变量y和x进行回归分析,得到一组样本数据(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是
A.由样本数据得到的回归方程 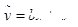 =bx+a必过点 =bx+a必过点 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数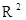 来刻画回归效果, 来刻画回归效果, 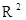 越小,说明模型的拟合效果越好 越小,说明模型的拟合效果越好 |
| D.若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系 |
若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是
A.91.5和91 .5 .5 |
B.91.5和92 |
| C.91和91.5 | D.92和92 |
在区间[1,3]上任取一数,则这个数大于1.5的概率为
| A.0.25 | B.0.5 | C.0.6 | D.0.75 |
①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名学生中抽取100名学生的样本;②某车间主任从20件产品中抽取7件样本进行产品质量检验.③从2000名学生中抽取10人了解平时的生活习惯.
以下几种随机抽样方法:I.简单随机抽样Ⅱ.系统抽样法;Ⅲ.分层抽样法.
上述三个问题和三种方法配对正确的是
| A.①配I,②配Ⅱ,③配Ⅲ | B.①配Ⅲ,②配Ⅱ,③配I |
| C.①配Ⅲ,②配I,③配Ⅱ | D.①配Ⅱ,②配I,③配Ⅲ |