已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将三角形AED折起，使DB=
，
如图，O，H分别为AE、AB中点．
（Ⅰ）求证：直线OH//面BDE； 
（Ⅱ）求证：面ADE
面ABCE；
（Ⅲ）求二面角O-DH-E的余弦值．
（本小题满分10分）已知定义域为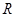
的函数
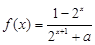是奇函数．
（1）求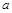
的值；
（2）若对任意的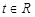
，不等式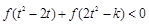
恒成立，求实数
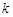的取值范围．
（本小题满分10分）如图是总体的一个样本频率分布直方图，且在[15，18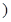
内频数为8．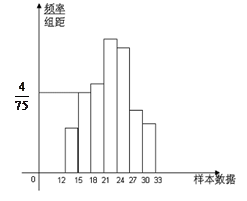
（1）求样本在[15，18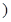内的频率；
（2）求样本容量；
（3）若在[12，15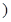内的小矩形面积为0.06，求在[18，33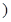内的频数．
对任意
，函数
的值恒大于零，求
的取值范围．
某学校校办工厂有毁坏的房屋一座，留有一面14m的旧墙，现准备利用这面墙的一段为面墙，建造平面图形为矩形且面积为126
的厂房（不管墙高），工程的造价是：
（1）修1m旧墙的费用是造1m新墙费用的25%;
（2）拆去1m旧墙用所得的材料来建1m新墙的费用是建1m新墙费用的50%.问如何利用旧墙才能使建墙的费用最低？
解关于x的不等式