有一堆形状大小相同的珠子,其中只有一粒质量比其他的轻,某同学经过思考,认为根据科学的算法,利用天平(不用砝码),二次称量肯定能找到这粒质量较轻的珠子,则这堆珠子最多有( )粒
| A.6 | B.7 | C.9 | D.12 |
已知函数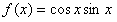 ,给出下列四个说法:
,给出下列四个说法:
①若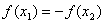 ,则
,则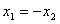 ;
;
② 的最小正周期是
的最小正周期是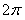 ;
;
③ 在区间
在区间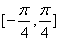 上是增函数;
上是增函数;
④ 的图象关于直线
的图象关于直线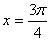 对称.
对称.
其中正确说法的个数为()
| A.1 | B.2 | C.3 | D.4 |
已知函数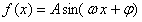
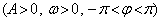 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为()
的解析式为()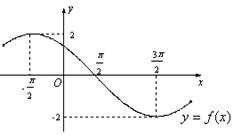
A.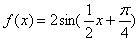 |
B.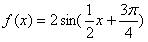 |
C.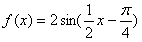 |
D.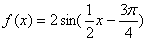 |
将函数 的图象按向量
的图象按向量 平移后得到图象对应的函数解析式是()
平移后得到图象对应的函数解析式是()
A. |
B. |
C. |
D. |
若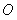 是
是 所在平面内的一点,且满足( BO+OC )•( OC-OA )=0,则
所在平面内的一点,且满足( BO+OC )•( OC-OA )=0,则 一定是()
一定是()
A. 等边三角形 B. 等腰直角三角形 C. 直角三角形 D. 斜三角形
设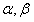 为两个平面,
为两个平面, 为两条直线,且
为两条直线,且 ,有如下两个命题:
,有如下两个命题:
①若 ;②若
;②若 . 那么()
. 那么()
| A.①是真命题,②是假命题 | B.①是假命题,②是真命题 |
| C.①、②都是真命题 | D.①、②都是假命题 |