(本小题12分)已知椭圆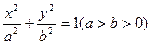 的左右焦点分别为
的左右焦点分别为 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形 是边长为2的正方形。
是边长为2的正方形。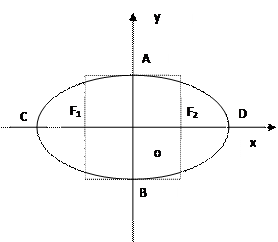
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点 。证明:
。证明: 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
第21题图
阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
请回答:BC+DE的值为_______.
参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
如图,在⊙ 中,
中,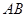 为直径,
为直径, ,弦
,弦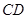 与
与 交于点
交于点 ,过点
,过点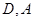 分别作⊙
分别作⊙ 的切线交于点
的切线交于点 ,且GD与
,且GD与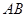 的延长线交于点
的延长线交于点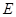 .
.
(1)求证: ;
;
(2)已知: ,⊙
,⊙ 的半径为
的半径为 ,求
,求 的长.
的长.
已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元;中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.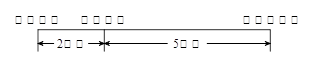
(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式;
(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F.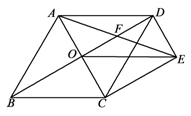
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩下的3支签中任意抽出1支签。
(1)用树状图或列表格等方法列出所有可能出现的结果;
(2)求抽出的两支签中,1支为甲签、1支为丁签的概率。