设
为实数,函数
。
(Ⅰ)求
的单调区间与极值;
(Ⅱ)求证:当
且
时,
。
(本小题满分12分)
如图,圆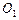 与圆
与圆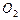 的半径
的半径 都等于1,
都等于1,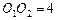 . 过动点
. 过动点 分别作圆
分别作圆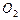 、圆
、圆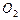 的切线
的切线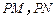 (
(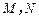 分别为切点),使得|PM|=|PN|.
分别为切点),使得|PM|=|PN|.
试建立适当的坐标系,并求动点 的轨迹方程.
的轨迹方程.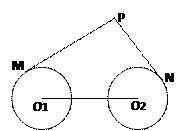
(本小题满分12分)
已知 ,
, ,若·=,
,若·=,
且 ,求
,求 的值
的值
(本小题满分12分)
已知数列 满足
满足
(Ⅰ)欲求 的通项公式,若能找到一个函数
的通项公式,若能找到一个函数

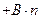
 (A、B、C未必常数),把递推
(A、B、C未必常数),把递推 关系变成
关系变成
 后,就容易求出
后,就容易求出 的通项了.请问:这样的
的通项了.请问:这样的 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么?
(Ⅱ)记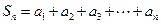 ,若不等式
,若不等式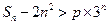 对任意
对任意 都成立,求实数
都成立,求实数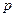 的
的 取值范围。
取值范围。
(本小题满分12分)
设 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过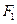 斜率为1的直线
斜率为1的直线 与
与
 相交于
相交于 两点,且
两点,且 成等差数列。
成等差数列。
(Ⅰ)求 的离心率;
的离心率;
(Ⅱ)设点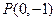 满足
满足 ,求
,求 的方程。
的方程。
(本小题满分12分)
已知函数
(Ⅰ)求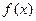 的单调区间;
的单调区间;
(Ⅱ )若
)若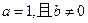 ,函数
,函数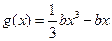 ,若对任意的
,若对任意的
 ,总存在
,总存在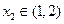 ,使
,使 ,求实数
,求实数 的取值范围。
的取值范围。