25.(18分)
如图所示,在0≤x≤a、0≤y≤ 范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B,坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内,已知粒子在磁场中做圆周运动的半径介于a/2到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的
范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B,坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内,已知粒子在磁场中做圆周运动的半径介于a/2到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的
(1)速度的大小; (2)速度方向与y轴正方向夹角的正弦.
已知氘核质量为2.0136 u,中子质量为1.0087u,He核的质量为3.0150u.
(1)写出两个氘核聚变成He核的反应方程;
(2)计算上述核反应中释放的核能;
(3)若两氘核以相等的动能0.35 MeV做对心碰撞即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的He核和中子的动能各是多少?
有一群氢原子处于量子数n=3的激发态,当它们跃迁时:
(1)这些氢原子最多能发出几种频率的光?并画出能级图,在图上用箭头标明;
(2)在哪两个能级间跃迁时,所发出的光子的波长最长?是多少?
(已知氢原子的基态能量E1=-13.6eV,量子数n的能级值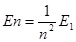 ,普朗克常数 h=6.63×10-34J·s)
,普朗克常数 h=6.63×10-34J·s)
质量m1=10g的小球在光滑的水平桌面上以v1=30cm/s的速率向右运动,恰好遇上在同一条直线上向左运动的另一个小球.第二个小球的质量为m2=50g,速率v2=10cm/s.碰撞后,小球m2恰好停止.那么,碰撞后小球m1的速度是多大,方向如何?
如图所示,在倾斜角α=37°的斜面上,有一质量为5kg的物体沿斜面滑下,物体与斜面的动摩擦因素μ=0.2,求物体下滑2s的时间内,物体所受各力的冲量。(g=10m/s2,sin37=0.6,cos37=0.8)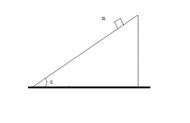
如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB是半径为d的 光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。求:
光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。(重力加速度为g)