已知以原点
为中心，
为右焦点的双曲线
的离心率
.
（Ⅰ）求双曲线
的标准方程及其渐近线方程；
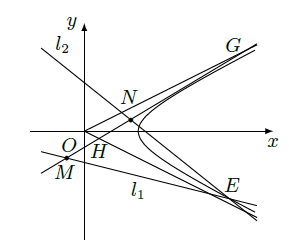
（Ⅱ）如题图，已知过点
的直线
与过点
（其中
）的直线
：
的交点
在双曲线
上，直线
与双曲线的两条渐近线分别交于
、
两点，求
的值.
求下列各组数据的方差与标准差（结果保留到小数点后一位）：
（1）1，2，3，4，5，6，7，8，9；
（2）11，12，13，14，15，16，17，18，19；
（3）10，20，30，40，50，60，70，80，90.
并分析由这些结果可得出什么一般性结论.
已知数列
满足：
，且存在大于1的整数k使
。
（1）用
表示m（不必化简）
（2）用k表示m（化成最简形式）
（3）若m是正整数，求k与m的值；
已知：经过点
的动圆与y轴交于M、N两点，C（-1，0），D（1，0）是x轴上两点，直线MC与
ND相交于P。
（1）求点P的轨迹E的方程；
（2）直线GH交轨迹E于G、H两点，并且
（O是坐标原点），求点O到直线GH的距离。
已知a为实数，函数
（I）若函数
的图象上有与x轴平行的切线，求a的取值范围；
（II）当
时，对任意
恒成立，试求m的取值范围。
袋中有大小相同的5个球，其中黑球3个，白球2个，甲乙二人分别从中各取一个，甲先取（不放回）乙后取。规定：
两人取到同颜色的球，由甲胜，取到不同颜色的球，则乙胜。
（1）分别求甲乙取到黑球的概率；
（2）甲乙二人谁胜的概率大，请说明理由。