如图1所示,宽度为的竖直狭长区域内(边界为),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为,表示电场方向竖直向上。时,一带正电、质量为的微粒从左边界上的点以水平速度射入该区域,沿直线运动到点后,做一次完整的圆周运动,再沿直线运动到右边界上的点。为线段的中点,重力加速度为。上述为已知量。
(1)求微粒所带电荷量和磁感应强度的大小;
(2)求电场变化的周期;
(3)改变宽度,使微粒仍能按上述运动过程通过相应宽度的区域,求的最小值。

(12分)我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大的提高了同学们对月球的关注程度。以下是某同学就有关月球的知识设计的两个问题,请你解答:
⑴若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
⑵若某位宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t,小球落回到抛出点。已知月球半径为R月,万有引力常量为G。试求出月球的质量M月。
如图所示,水平转台上有一个质量m=5kg的小物体,一根劲度系数k=103N/m、原长为8cm的弹簧一端连接转台中心的转轴,另一端连接此物体。当整个装置处于静止时,弹簧的长度为10cm。如果小物体与转台之间的摩擦足够大,讨论:
(1)要使小物体与转台之间不存在摩擦力,则转台转动的角速度应为多大?
(2)要使小物体与转台之间的摩擦力大小为5N,则转台转动的角速度又应为多大?
如图所示,木板B的质量M="2" kg,与右墙距离为S.物体A(可视为质点)质量m="l" kg,以初速度v0="6" m/s从左端水平滑上B.己知A与B间的动摩擦因数μ=0.2,在B第一次撞墙前,A已经与B相对静止.地面光滑,B与两面墙的碰撞都是弹性的。求: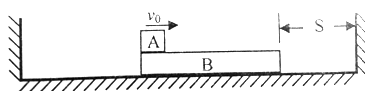
①S的最小值:
②若A始终未滑离B,A相对于B滑行的总路程是多少?
一根弹性绳沿x轴方向放置,左端在原点O处,用手握住绳的左端使其沿y轴方向做周期为1 s的简谐运动,于是在绳上形成一列简谐波,振动传播到质点M时的波形如图所示.绳上质点N的平衡位置为x="5" m,求:
①波从O传到N的过程中,O点通过的路程;
②如果从N开始振动计时,画出质点N振动的位移—时间图线.
如图所示,一个开口向上的圆筒气缸直立于地面上,距缸底2L处固定一个中心开孔的隔板a,在小孔处装有一个能向下开启的单向阀门b,只有当上部压强大于下部压强时,阀门才开启.C为一质量与摩擦均不计的活塞,开始时隔板以下封闭气体压强为1.2p0 (p0为大气压强);隔板以上由活塞c封闭的气体压强为p0,活塞C与隔板距离为L.现对活塞c施加一个竖直向下缓慢增大的力F0设气体温度保持不变,已知F增大到F0时,可产生向下的压强为0.2p0,活塞与隔板厚度均可不计,(上下是相同的理想气体)求: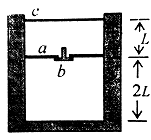
①当力缓慢增大到2F0时,活塞c距缸底高度是多少?
②当力缓慢增大到4F0时,缸内各部分气体压强是多少?